Hallo Marco,
Du schreibst, dass $$\vec{F} = F\begin{pmatrix} 1 \\ 1 \end{pmatrix}$$ gegeben ist. Stimmt das so? IMHO müsste es eher heißen: $$\vec{F} = F \frac12 \sqrt{2}\begin{pmatrix} 1 \\ 1 \end{pmatrix}$$ ... aber belassen wir es mal dabei! Weiter ist gegeben: $$ \quad \vec{F} = \vec{F_1} + \vec{F_2}$$ ich nutze bewusst die Schreibweise mit dem Pfeil darüber, um den Kraftvektor von der Größe der Kraft zu unterscheiden.
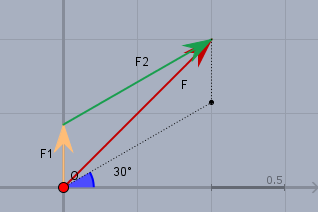
Das \( \vec{F} = \vec{F_1} + \vec{F_2}\) steht für eine Vektoraddition der beiden Kraftvektoren \(F_1\) (okerfarben) und \(F_2\) (grün), die zusammen \(F\) (rot) ergeben. Wobei es egal ist, ob man \(\vec{F} = \vec{F_1} + \vec{F_2}\) schreibt, - so wie im Bild zu sehen - oder \( \vec{F} = \vec{F_2} + \vec{F_1}\). Im zweiten Fall würde sich der grüne Pfeil auf der gepunkteten Linie unterhalb von \(F\) befinden und der okerfarbene rechts.
Nun, man soll die Kräfte zerlegen, die schon eigentlich zerlegt sind, in F1 und F2? weswegen ich irgendwie die Frage schon nicht verstehe.
\(\vec{F}\) soll in die Anteile \(\vec{F_1}\) und \(\vec{F_2}\) zerlegt werden. Nicht mehr und nicht weniger.
Ich habe hier kein Winkel gegeben, wobei ich bei F2 einen Winkel habe, wie soll ich dann F1 zerlegen
\(\vec{F_1}\) steht ja offenbar senkrecht, d.h. sein Winkel gegenüber der Horizontalen (X-Achse) ist 90°.
Nun zur eigentlichen Rechnung:
Ganz allgemein kann man für eine Kraft \(\vec{K}\) schreiben, die um den Winkel \(\varphi\) gegenüber der X-Achse gedreht ist:
$$\vec{K} = K \cdot \begin{pmatrix} \cos \varphi\\ \sin \varphi \end{pmatrix}$$ d.h. $$\vec{F_1} = F_1 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix}; \quad \vec{F_2} = F_2 \cdot \begin{pmatrix} \cos 30° \\ \sin 30° \end{pmatrix} = F_2 \cdot \begin{pmatrix} \frac12 \sqrt{3} \\ \frac12 \end{pmatrix}$$
Oder wird hier wirklich nach der x und y Komponente gefragt? Müsste ich theoretisch nicht F1 in Fx und Fy zerlegen?
Nein - \(F_1\) kann man nicht in \(F_x\) und \(F_y\) zerlegen, sondern höchsten in \(F_{1x}\) und \(F_{1y}\). Aber das ist hier nicht gefragt.
Man soll nur die Beträge von F1 und F2 angeben.
schreibst Du selber (s.o.). Und dies ist genau das, was ich mit \(F_1\) und \(F_2\) bezeichnet habe. Und das lässt sich berechnen, wenn man die Kräfte als Vektoren in die Summengleichung einsetzt:
$$\vec{F} = \vec{F_1} + \vec{F_2} = F_1 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} + F_2 \cdot \begin{pmatrix} \frac12 \sqrt{3} \\ \frac12 \end{pmatrix} = F\begin{pmatrix} 1 \\ 1 \end{pmatrix}$$ Dies ist jetzt ein lineares Gleichungssystem mit zwei Gleichungen (in X- und Y-Richtung) und zwei Unbekannten (\(F_1\) und \(F_2\)). Aus der ersten Gleichung folgt bereits \(F_2\): $$F_2 \frac12 \sqrt{3} = F; \quad \Rightarrow F_2 = \frac23 \sqrt{3} F \approx 1,155F$$
Einsetzen in die zweite Gleichung und auflösen nach \(F_1\) gibt dann $$F_1 + \frac12 F_2 = F\\ \space \Rightarrow F_1 = F - \frac12 F_2 = F - \frac13 \sqrt{3} F = \left( 1 - \frac13 \sqrt{3}\right) F \approx 0,423 F$$ Ein Vergleich der Werte mit den Längen in der Skizze zeigt, dass die Werte sinnvoll sind.
Gruß Werner