Guten morgen,
ich habe folgende Aufgabe und verstehe nicht warum nicht auch Antwortmöglichkeit D (F2, F4) richtig sein kann.
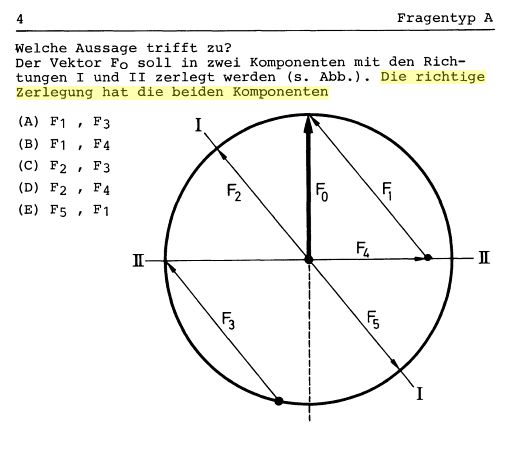
Die Vektoren F2 und F4 würden doch auch ein Parallelogramm mit F1 bilden.
Ich habe 2 Allgmeine Regeln für die "komponentenzerlegung" gelesen, welche meiner Meinung nach hier auch auf Antwortmöglichkeit D) zutreffen ( - oder nicht ?)
1.) Vektoren können parallel verschoben werden
2.) Diagonale ders Paralellogramms ist Ursprungsvektor
--------------------------------------------------------------------------------------------------------
Dann noch eine Verständnisfrage: Ich habe gelesen, dass gilt :
Summe der Komponenten = ursprünglicher Vektor
Was ist damit gemeint ?
PS: Bitte einfach erklären :D Ist eigentlich eine allgemeine Physikfrage .