Für den Abstand der resultierenden Kraft benötigst Du natürlich alle Momente. Diese ergeben sich aus dem Kreuzprodukt Hebelarm mal Kraftvektor. Es ist:
$$M_{1,0} = \begin{pmatrix} -1 \\ 3 \end{pmatrix} \text{m}\times \begin{pmatrix} -3 \\ -1 \end{pmatrix} \text{N} = 10\text{Nm}$$
$$M_{2,0} = \begin{pmatrix} 1 \\ 4 \end{pmatrix} \text{m}\times \begin{pmatrix} 1 \\ -4 \end{pmatrix} \text{N} = -8\text{Nm}$$
$$M_{3,0} = \begin{pmatrix} -1 \\ 1 \end{pmatrix} \text{m}\times \begin{pmatrix} 2 \\ 2 \end{pmatrix} \text{N} = -4\text{Nm}$$
$$M_{4,0} = \begin{pmatrix} 1 \\ -5 \end{pmatrix} \text{m}\times \begin{pmatrix} 4 \\ 2 \end{pmatrix} \text{N} = 22\text{Nm}$$
Daraus folgt dann die Summe aller Momente
$$\sum_{i=1}^4 M_{i,0}=20\text{Nm}$$
Die Summe aller Kräfte ist
$$\sum_{i=1}^4 F_i= \begin{pmatrix} 4 \\ -1 \end{pmatrix} \text{N} \quad \Rightarrow \space \left| \sum_{i=1}^4 F_i\right| = \sqrt{17} \text{N}$$
Demzufolge ist der Hebelarm \(r\) - also der Abstand dieser Kraft vom Koordinatenursprung
$$\left| \sum M_i \right| = r \cdot\left|\sum F_i \right| \quad \Rightarrow \space r = \frac{20\text{Nm}}{\sqrt{17} \text{N}}=\frac{20}{17}\sqrt{17} \text{m} \approx 4,851 \text{m}$$
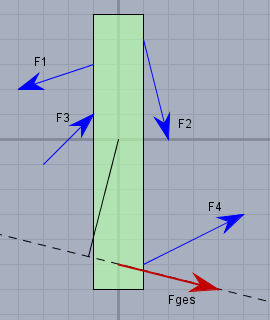
Im obigen Bild habe ich die Gesamtkraft (rot) mit der berechneten Entfernung eingezeichnet. Die Wirkungslinie der Kraft geht durch den Punkt \((0;-5)^T\). Kontrollrechnung:
$$\sum_{i=1}^4 M_{i,0}= \begin{pmatrix} 0 \\ -5 \end{pmatrix} \text{m} \times \begin{pmatrix} 4 \\ -1 \end{pmatrix} \text{N} = 20 \text{Nm} $$
scheint also richtig zu sein.
Gruß Werner