Hallo mistermathe,
Du fragst: " .. aber warum ist G bei den Lösungen - G" Das ist die Konvention bei den Vorzeichen. Das resultierende Moment \(M\) ist rechts drehend - also definitionsgemäß negativ. Ersteres folgt aus der Anschauung (s. mein Kommentar zu Deinem letzten Posting). Da \(G\) und \(l\) als positive Werte angenomen sind, kommt vor das Ergebnis ein Minuszeichen.
Du schreibst: "Bei den restlichen Arten komme ich gar nicht klar." Bei a), c) und d) ist es im Grunde ganz einfach, wenn man sich überlegt, dass es dem Balken völlig egal ist, auf welche Weise das Gewicht \(G\) an ihm befestigt ist. Hauptsache es befindet sich von der Einspannstelle aus gesehen in der Horizontalen - also des Abstands der Wirkungslinie der Gewichtskraft \(G\) - immer gleich weit entfernt. Das Ergebnis ist immer \(M=-l \cdot G\). Auch bei c) hat das einlaufenden Seil an der Einspannstelle keine Möglichkeit ein zusätzliches Moment aufzubauen, was daran etwas ändert.
Bei b) ist es anders, da hier ein Moment von der Befestigungsstelle des Seils aus aufgebaut wird. Denke ich mir das gesamte Gebilde im Punkt \(O\) festgeschraubt, so wirkt ohne Zweifel hier das Moment \(-l\cdot G\).
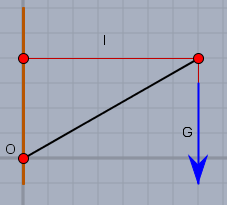
Schneide ich aber die Einspannstelle frei, so wirkt auch die waagerechte Seilkraft auf den Balken und erzeugt das Moment \(h \cdot G\) - und das ist diesmal positiv, links drehend.
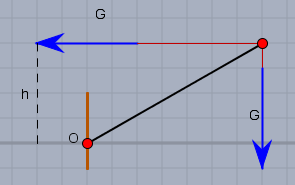
Das Moment an der Einspannstell ist demnach \(M=-l\cdot G + h \cdot G\).
Zur Frage: "versteh ich nicht was die in der Aufgabe mit ` Ebenso kann das Eigengewicht der Komponenten außer Acht gelassen werden` meinen" Mit 'Komponenten' ist der Balken, bzw. Winkelbalken selbst gemeint. Ist das Gewicht dieser Konstruktion gegenüber \(G\) ausreichend klein, so kann es vernachlässigt werden.