Auflagekräfte bei einem Balken bestimmen, mit Streckenlast

Question

Hallo, kann mir jemand helfen, wie ich die Lagerreaktion ermitteln kann?

Ich habe einen Ansatz, weiß jedoch nicht mehr weiter.

Ich habe nämlich einige Fragen und weiß nicht was ich ganz genau beachten soll. Wenn ich meine ausgerechneten Ergebnisse in die Gleichgewichtsbedingung reinschreibe, in der 0 rauskommen muss, kommt leider keine 0 raus. Vielleicht kann ja einer von euch meinen Fehler sehen:

 Wenn ich die horizontale Kraft berechnen will stelle ich folgendes auf:

$$\rightarrow Bx-Fx=0\\ \rightarrow Bx=\quad F*cos(45)=\quad \sqrt { 2F } *\frac { \sqrt { 2 }  }{ 2 } \\ \rightarrow Bx=F$$

Die Vertikalen Kräfte, brauche ich auch nicht aufstellen, da auch hier zu viele unbekannte vorhanden sind. Daher drehe ich um den Punkt B:

Bevor ich das mache, bestimme ich die Resultierende Kraft, bei der ich mir nicht wirklich sicher bin, ob dies richtig ist:

für q0, habe ich 2F/a gegeben, so habe ich das dann eingesetzt. Ich glaube die Resultierende lässt sich wie folgt bestimmen:

R=q0*L oder?

$$R=q0*l=\frac { 2F }{ a } *a=\quad 2F?$$

so habe ich wenn ich einen Moment, um den B mache, folgendes raus:

$$\curvearrowright B:2F*a+2F*2a+Fy*3a+Ay*3a=0\\ Ay=\frac { 9Fa }{ 3a } =3F$$

$$Fy=\quad \sqrt { 2F } *\frac { \sqrt { 2 }  }{ 2 } =F$$

Hier war ich mir unsicher, was für einen Hebelarm ich für die Streckenlast nehmen sollte, da die Resuliterende bei a/2 liegt und nicht bei a, oder 2a, bei der anderen Streckenlast. Ich habe dies zwei mal berechnet, zwei verschiedene Werte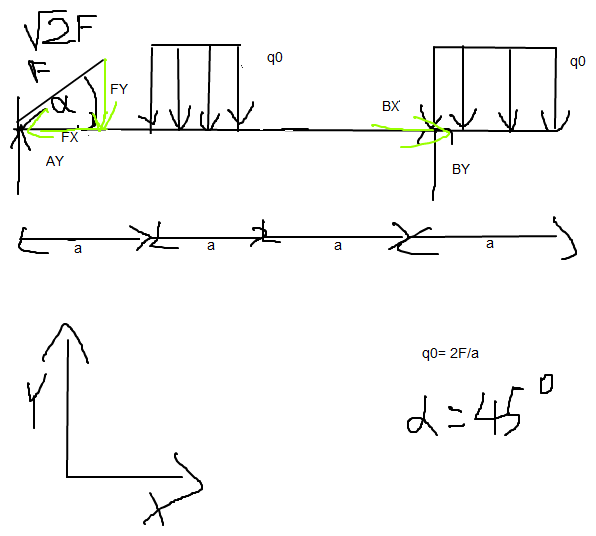 rausbekommen. Beide in die Probe-Formel eingesetzt, trotzdem keine 0 rausbekommen. Ich hoffe das mir jemand sagen kann, wo hier der Fehler liegen könnte.

LG Tekto

Answer 1

Hallo Tekto,

(war gerade verhindert ...)

Deine Aufgabe ist leider ungenau beschreiben. Ich gehe davon aus, dass es sich dabei um einen Biegebalken handelt. Leider ist unklar, wie er gelagert ist. Wenn in den Punkten \(A\) und \(B\) sowohl Vertikal- (Y) als auch Horizontalkräfte (X) in den jeweiligen Lager aufgenommen werden könne, so wäre er überbestimmt gelagert.

Ich gehe mal der Einfachhalt halber davon aus, dass \(A\) ein Gleitlager ist; d.h. \(A_x=0\). Ein \(A_x\) kommt bei Deiner Rechnung nicht vor. Somit ist der Teil mit \(B_x\) korrekt.

Die resultierenden Kräfte in Y-Richtung kannst Du ruhig aufstellen. Es ist

$$F_y + 2(q_0 \cdot a) - A_y - B_y = 0$$ hier sind zwar \(A_y\) und \(B_y\) unbekannt, aber Du erhältst so bereits einen Zusammenhang zwischen beiden.

Das Moment um \(B\) ist so nicht richtig. Das Moment dreht mathematisch positiv, d.h. von X nach Y. Die rechte Streckenlast hat einen Hebel von \(a/2\) und dreht negativ. Der Hebel ist im Schwerpunkt der Streckenlast anzusetzen. Die linke Streckenlast und \(F_y\) drehen positiv und \(A_y\) wieder negativ. \(F_x\) hat keinen Einfluss. Somit ist das Moment um \(B\): $$M_B = -\frac{a}{2} R + \frac{3a}{2} R + 3F_y - 3 A_y= 0$$ in dieser Gleichung ist lediglich \(A_y\) unbekannt. Ich löse danach auf:

$$A_y = \frac13(a \cdot R + 3F_y) = \frac{a}{3}R + F_y = \frac23 F + F = \frac53 F$$ setzt man diese in Kräftesumme in Y ein (s.o.), so erhält man: $$F_y + 2(q_0 \cdot a) - \frac53 F - B_y = 0$$ $$\Rightarrow B_y = F + 4F - \frac53F = \frac{10}{3}F$$ Deine Fehler liegen in der Wahl des Vorzeichens der rechten Streckenlast und \(A_y\) und die Resultierende der Streckenlast musst Du natürlich in den Schwerpunkt der Streckenlast setzen.

Gruß Werner

Comments

Hallo Werner,

vielen Dank!

Ein paar Verständnis Fragen:

Als du alle Kräfte in Richtung Y Richtung aufgestellt hast, hast du dich dann glaub ich nicht nach dem vorgegebenen Koordinatensystem gehalten, oder?

Laut diesen sind ja alle Kräfte positiv die nach oben gehen und bei den resultierenden und Fy Komponente wäre es ja in dem Fall negativ oder?

Am Endeffekt wäre es eh nur ein Vorzeichen Fehler, will nur sicher gehen ob ich es auch richtig verstanden habe von dir habe von dir sehr viel gelernt!

Ich habe alles verstanden, ich würde nur gerne wissen wollen, wieso die Rechte Streckenlast, doch nicht positiv ist wenn ich nach rechts drehe? Wenn ich meinen Moment um Punkt B nach rechts drehe, geht doch die resultierende mit nach unten , in dem Fall positiv oder sehe ich hier irgendwas falsch? Für mich wäre die resultierende negativ wenn sie nach oben gehen würde und ich meinen Moment noch immer nach rechts drehe.

Ansonsten alles verstanden ‚ top Danke!!!

Viele Grüße

Tekto

---

Hallo Tekto,

Als du alle Kräfte in Richtung Y Richtung aufgestellt hast, hast du dich dann glaub ich nicht nach dem vorgegebenen Koordinatensystem gehalten, oder?

Gut erkannt. Spielt aber keine Rolle! Multipliziere die Gleichung mit \(-1\) und alles ist gut.

... ich würde nur gerne wissen wollen, wieso die Rechte Streckenlast, doch nicht positiv ist wenn ich nach rechts drehe?

Ein Bild dazu:

 

Mathematisch positiv ist eine Links-Drehung. Also von der X- zur Y-Achse. Wobei es hier (wie bei den Kräften) letztlich nur darauf ankommt, dass die Vorzeichen zueinander stimmig sind. D.h. das Vorzeichen des Moments der rechten Streckelast ist ein anderes wie das linke.

Links (positiv) um \(B\) drehen: \(M_{B+} = \frac32 aR + 3F_y\)

Rechts (negativ) um \(B\) drehen: \(M_{B-} = \frac12 aR + 3aA_y\)

Am Ende des Tages muss immer gelten: \(M_{B+} = M_{B-}\)

---

Hallo Werner,

alles klar! Das habe ich vergessen! Ich sollte das dann von dem Punkt aus betrachten. Danke.