Kräfte bestimmen, 2 Beispiele mit Streckenlast

Question

 

Man kann doch sagen, dass im ersten Fall, F_A=F_B=F aufgrund der Symmetrie ist oder?

Wenn man im zweiten Fall die Streckenlast zu einer Resultierenden zusammenfassen würde, also F=q_0 *2L, kann man dann sagen, dass F_A=F_B=q_0 L ist oder geht es nicht aufgrund der Streckenlast?

Answer 1

Hallo probe,

Du fragst "dass im ersten Fall, F_A=F_B=F aufgrund der Symmetrie ist - oder?" Ja - das ist so. Du kannst das auch leicht nachprüfen. Momentensumme um \(A\) gibt

$$-L \cdot 2F + 2L \cdot F_B = 0 \quad \Rightarrow F_B=F$$

Zu Deiner zweiten Frage: Ja - Du kannst eine Streckenlast durch ihre Summe, die im Schwerpunkt der Streckenlast wirkt, ersetzen. Zumindest für die Bestimmung der Schnitt- und Lagerkräfte, die sich außerhalb(!) der Streckenlast befinden. Das ist hier der Fall.

Gruß Werner

Comments

Vielen Dank. Für den zweiten Fall gilt also:

F_A=F_B=q_0 L wegen der Symmetrie?

Zu Deiner zweiten Frage: Ja - Du kannst eine Streckenlast durch ihre Summe, die im Schwerpunkt der Streckenlast wirkt, ersetzen. Zumindest für die Bestimmung der Schnitt- und Lagerkräfte, die sich außerhalb(!) der Streckenlast befinden. Das ist hier der Fall. 

Was meinst Du damit?

---

Nimm das Bild mit der Strecklast und ersetze die Streckenlast durch eine Punktlast in der Mitte des Balkens. Wenn Du anschließend z.B. die Querkraft in der Mitte des Balkens mittels Freischneiden bestimmst, so machst Du einen Fehler, da die Mitte des Balkens innerhalb der Streckenlast liegt, die zu einer einzelnen Kraft zusammen gefasst wurde und dann keine Rolle mehr spielt!

---

mhh verstehe das irgendwie nicht.

Mir ist klar, dass man eine Streckenlast durch eine Punktlast zusammenfassen kann, das heißt in diesem Fall, F_res=2L*q_0.

Wenn ich jetzt die Auflagerreaktionen bestimmen möchte rechts und links, kann ich wie im Fall 1 sein, dass wegen der Symmetrie gilt F_A=F_B=q₀*L.

---

"Wenn ich jetzt die Auflagerreaktionen bestimmen möchte rechts und links, kann ich wie im Fall 1 sein, dass wegen der Symmetrie gilt F_A=F_B=q0*L. " Ja  - das ist völlig ok.

Ich versuche mein obige Schilderung noch mal. Was ist wenn Du im Fall 2 (der mit der Streckenlast) die Querkraft innerhalb des Balkens bestimmen willst? Hier ersetze ich zunächst die Streckenlast durch eine Punktlast in der Mitte des Balkens.

 

mal angenommen, Du schneidest nun rechts von der Mitte den Balken und stellst die Kräftesumme in Y für den rechten Teil auf, dann erhältst Du \(Q=F_B\). Das wäre aber falsch, da rechts von der Mitte auch noch die Streckenlast wirkt, die nun in einer Punktlast zusammen gefasst ist.

---

Nehmen wir an von A nach B beträgt die Länge L. Wenn man ein jetzt Q(x=L) bestimmen will, kann man sagen Q(x=L)=Fb oder geht das auch nicht??

---

"Nehmen wir an von A nach B beträgt die Länge L. Wenn man ein jetzt Q(x=L) bestimmen will, kann man sagen Q(x=L)=Fb oder geht das auch nicht??" das geht schon, da \(Q(x=L)\) sich wieder außerhalb der Streckenlast befinden würde.

Möchtest Du aber z.B. \(Q(x=2L/3)\) berechnen, so musst Du die Streckenlast berücksichtigen; ein Ersatz der Streckenlast durch eine Punktlast in der Mitte wäre dann verkehrt.

---

Vielen Dank bist mir eine große Hilfe. Jetzt ist es mir klar.

Falls es noch dazu kommt, dass ich dazu eine kleine Frage habe, kann ich mich bitte  hier unten wieder melden?

---

... Du kannst Dich natürlich immer melden. Dafür ist dieses Forum da. Wenn Du Dich hier meldest bekomme ich das auch mit. Ich bin nur nicht immer da! Nächstes WE z.B. bin ich 3 Tage offline.

---

Alles klar :)

Das hier geht auch oder:

Q(x=L/2) = -q₀L.

Es geht um das letzte eingefügte Bild von Dir im Kommentar...

---

Zum Verständnis noch:

"Nehmen wir an von A nach B beträgt die Länge L. Wenn man ein jetzt Q(x=L) bestimmen will, kann man sagen Q(x=L)=Fb oder geht das auch nicht??" das geht schon, da Q(x=L) sich wieder außerhalb der Streckenlast befinden würde

Theoretisch wirkt doch an der Stelle L auch die Streckenlast, die ist doch überall verteilt....?

---

"Das hier geht auch oder: Q(x=L/2) = -q0L." Nein - richtig wäre \(Q(x=L/2)=0\). Überlege mal wieso das so sein muss!

---

Ich gehe aber davon aus, dass bei x=L/2 die zusammenfassende Punktlast ist...

Die Streckenlast geht doch von A bis B...

---

Ja - das ist doch genau der Fehler. Wenn Du Kräfte und Momente bestimmen willst, die innerhalb der Streckenlast liegen - und die Stellen \(x=L/2\) oder \(x=2L/3\) liegen innerhalb des Intervalls - dann darfst Du die gesamte Streckenlast nicht durch eine Punktlast ersetzen. Die Streckenlast geht von A bis B richtig, und die Punkte A und B liegen folglich außerhalb. Dort kannst Du durch die Punktlast ersetzen.

Oben habe ich den Balken bei \(x=L/2\) frei geschnitten, ich betrachte nur den Teil rechts der Mitte. Die vertikale Kräftesumme (in Z) gibt \(Q(x=L/2)=0\) wenn ich die Streckenlast rechts der Mitte berücksichtige!

---

Okay, irgendwas mache ich dann hier falsch:

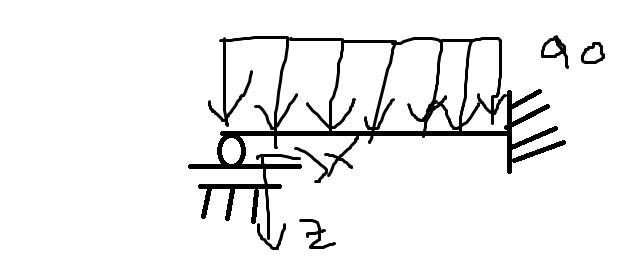 Die Länge des Balkens ist L. Die Zeichnung ist mir leider nicht so gut gelungen. Ich hoffe aber trotzdem, dass Du weißt was ich meine...Wenn ich die Biegelinie bestimmen will und ich nehme als Bedingungen:

w(x=0)=0

w(x=L)=0

w"(x=0)=0

w´(x=L)=0

EIw^IV(x)=q₀ Ich nenn dass einfach mal q

EIw(x)=q*x⁴ /24+C₁x³/6+C₂x²/2+C₃x+C4

C₁=-3*q*L/8

Wenn ich aber folgende Bedingung nehme EIw^III(x=0)=C₁=-q*L/2, komm ich für C1 wie Du siehst auf etwas anderes. Was habe denn falsch verstanden..

Ich brauche echt dringend Hilfe :)

---

Hallo probe,

das hat jetzt aber nicht unbedingt etwas mit unserer bisherigen Diskussion zu tun. Besser wäre es gewesen, Du hättest eine neue Frage aufgemacht.

Was ist das 'Elw(x)'? Wie kommst Du auf \(C_1=-3 \cdot q \cdot L/8\)?

---

Doch hat es eigentlich schon.

Kennst Du dich mit der Biegelinien DGL aus?

E ist das Elastizitätsmodul

I soll das Flächenträgheitsmomet sein

w(x) die Duechbiegung an der Stelle x

Es geht darum die Konstanten mithilfe der Randbedingungen zu bestimmen, verstehst du die Randbedingungen, dann verstehst du auch wahrscheinlich mein Problem

Allgemein gilt auch

EIw^III(x)=-Q(x)

EIw^II(x)=-M(x)

Sagt dir das alles was?

---

"Doch hat es eigentlich schon"  Ich dachte wir diskutieren darüber, ob und wann man Streckenlasten zu einer Punktlast zusammen fassen kann/darf.

"Sagt dir das alles was?" ja schon, aber ich mache jetzt gleich Schluss. Ich müsste mich da nochmal rein denken. Ich melde mich ggf. morgen wieder.

---

Ja schon.... wenn ich halt eine Bedingung mache mit der Querkraft, wo ich die Streckenlast nicht benutzte komme ich auf ein anderes Ergebis als wenn man es mit einer andere Bedingung macht. Nun die Frage welche Bediungen stimmen.