Hallo probe,
Die 'Rechte-Hand-Regel' hat Dir Lu schon beantwortet. Bei Wikipedia gibt es auch schöne Bilder dazu.
Du fragtest noch "Ich habe nur Probleme bei den Momenten in x und y, wie bestimme ich die Vorzeichen...." Ich zeichne das noch mal als Schrägriss auf, damit wir über das gleiche reden.
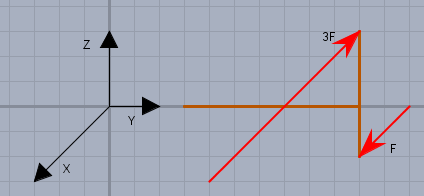
Das wichtigste ist hier immer zunächst die Koordinatenrichtungen fest zu legen. Das hast Du nicht gemacht. In meiner Skizze schaut die X-Achse aus dem Bild heraus, die Y-Achse nach rechts und Z nach oben!
Die Kraft \(3F\) wirkt in negative X-Richtung, die Kraft \(F\) wirkt in positive X-Richtung. Wenn Du Dir nun obige Skizze anschaust, dann stelle Dir vor, es wird von links nach rechts eine Schraube in Y-Richtung hinein gedreht. Das ist die positive Richtung für alle Momente um die Y-Achse. Das Moment, was an der Schnittstelle auf die Struktur wirkt, sei \(M_y\) bzw. \(M_y(y)\), wenn das Moment sich mit \(y\) verändern sollte; tut es aber hier nicht. die Kraft \(3F\), die in negative X-Richtung wirkt hat einen positive Hebel in Z-Richtung, d.h. sie dreht gegen die Schraubrichtung, ist also negativ. Die Kraft \(F\) in X-Richtung wirkt zwar gegenläufig, aber ihr Hebel hat eine negative Z-Koordinate, das daraus resultierende Moment wirkt also auch gegen die Schraubrichtung, d.h. negativ - daher
$$\sum M_Y = M_y - \frac35 b \cdot 3F - \frac25 b \cdot F$$
Rein formal kannst Du Momente auch ganz allgemein mit Hilfe des Kreuzprodukts beschreiben. Ich suche noch mal eine meiner früheren Antworten und melde mich nochmal.
Gruß Werner