Aufgabe:
Alles hat geklappt.
Bei der b) gab es etwas Probleme beim Berechnen des Widerstandes R1.
Ich verstehe den Weg wie man darauf kommt, aber wieso kann man für Usensor und Ua einfach die Werte in die Formel (rot markiert) aus dem Diagramm einsetzen, von t=0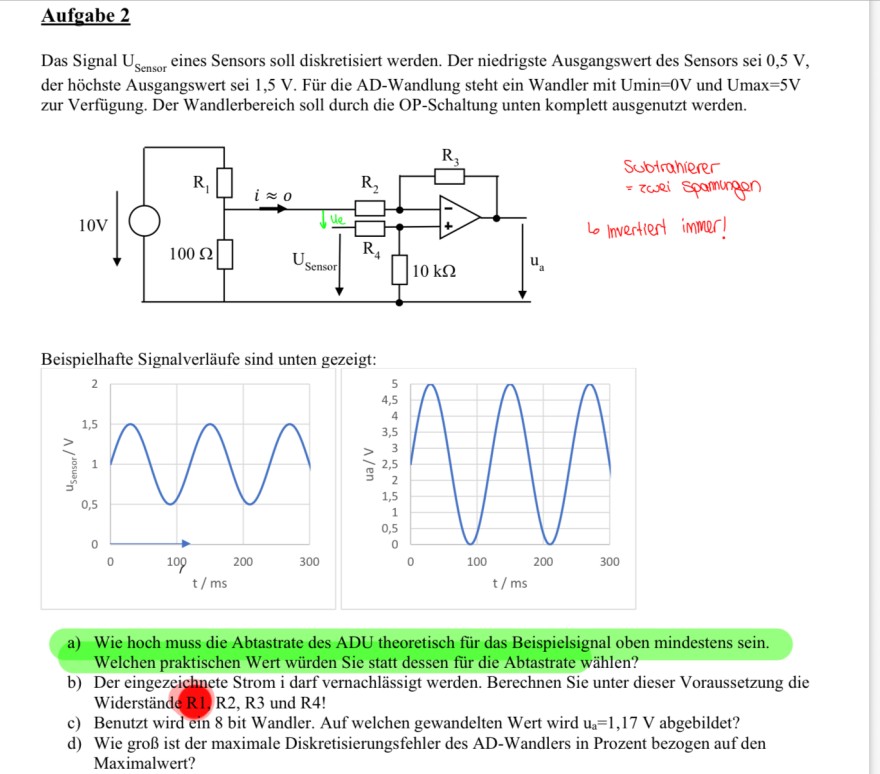
Text erkannt:
Aufgabe 2
Das Signal \( \mathrm{U}_{\text {Sensor }} \) eines Sensors soll diskretisiert werden. Der niedrigste Ausgangswert des Sensors sei \( 0,5 \mathrm{~V} \), der höchste Ausgangswert sei \( 1,5 \mathrm{~V} \). Für die AD-Wandlung steht ein Wandler mit Umin \( =0 \mathrm{~V} \) und Umax \( =5 \mathrm{~V} \) zur Verfügung. Der Wandlerbereich soll durch die OP-Schaltung unten komplett ausgenutzt werden.
\( \begin{array}{l} \text { Subtrahierer } \\ \text { = zwei spamungen } \end{array} \) Lo Invertient immer!
Beispielhafte Signalverläufe sind unten gezeigt:
a) Wie hoch muss die Abtastrate des ADU theoretisch für das Beispielsignal oben mindestens sein. Welchen praktischen Wert würden Sie statt dessen für die Abtastrate wählen?
b) Der eingezeichnete Strom i darf vernachlässigt werden. Berechnen Sie unter dieser Voraussetzung die Widerstände R1, R2, R3 und R4!
c) Benutzt wird ein 8 bit Wandler. Auf welchen gewandelten Wert wird \( \mathrm{u}_{\mathrm{a}}=1,17 \mathrm{~V} \) abgebildet?
d) Wie groß ist der maximale Diskretisierungsfehler des AD-Wandlers in Prozent bezogen auf den Maximalwert?

Text erkannt:
(1) \( f_{5}>2 \cdot f_{0} \)
\( \begin{array}{l} f_{0}=\frac{1}{T}=\frac{2,5}{200 \mathrm{~ms}}-\frac{2,5}{0,35}=8, \overline{3} \mathrm{~Hz} \\ f_{s}>2.8,5 \mathrm{th} \\ f_{s}>16 . \overline{6} \mathrm{Hk} \\ f_{\text {s.poris }}>10 . f_{0} \\ \text { fsiproxis }>10,8, \overline{3} \mathrm{~Hz} \\ >83.3 \mathrm{HK} \end{array} \)
\( \rightarrow \) Tasten wir Eingangssignal oder Auspangssignal ab?
- Wern beide Sgrade dieselve Frequenzinformation entralten (weine Frequenzänderung), damn ist es egal. welches abgetastet wirl
- wenn Frequenz sion andert, moss das Signal apagetastet werlen, das in ADU eingespeist wird
b) \( R_{3}=10 \mathrm{k} \Omega \)
\( \begin{array}{ll} V=\frac{R_{3}}{R_{2}} \quad V & =\frac{u_{1}, P P}{u_{1} P P}=\frac{5 V}{1 V}=5 \\ V & =\frac{R_{3}}{R_{2}} \\ R_{2} & =\frac{R_{3}}{Y_{0}} \\ R_{2} & =\frac{Y_{0}}{5} \\ R_{2} & =2 k_{1} \Omega \\ & =R_{4} \end{array} \)
\( \begin{aligned} R_{1}: \quad u_{a} & =\frac{R_{3}}{R_{1}} \cdot\left(u_{\text {serisor }}-v_{\text {Bias }}\right) \\ u_{a} \cdot \frac{R_{2}}{R_{3}} & =u_{\text {Sersor }}=u_{\text {Bias }} \\ u_{\text {Bias }} & =-u_{a} \frac{R_{2}}{R_{3}}+u_{\text {Sersor }} \\ u_{\text {Bias }} & =-2,5 \mathrm{~V} \cdot \frac{2 R_{n}}{10 u_{3}}+\Lambda \mathrm{V} \\ u_{\text {Bias }} & =0,5 \mathrm{~V} \end{aligned} \)
c) \( n=8 \mathrm{Bit} \)
\( \begin{array}{l} u_{a}=\text { runden }\left(\frac{u-u m i n}{L S B}\right) \cdot L S B+u m i n \\ L_{S B}=\frac{u_{\max }-u m}{a^{n}-1} \\ 5 v-o v \end{array} \)
Spannunosteiler - Regel:
\( \begin{array}{l} U_{\text {R100 }}=U_{\text {AgS }} \frac{R_{\text {R100 }}}{R_{\text {Roon }}+R_{1}} \\ 05 \mathrm{~V}=10 \mathrm{~V} \cdot \frac{100 \Omega}{100 \Omega+14} \\ 100 \mathrm{e}+\mathrm{R}_{1}=\frac{10 \mathrm{~V}}{95 \mathrm{~V}} \cdot 100 \mathrm{e} \\ R_{1}=\frac{10 \mathrm{~V}}{0,5 \mathrm{~V}} \cdot 100 \mathrm{e}-100 \mathrm{e} \\ R_{1}=1900 \Omega \end{array} \)