Aufgabe:
Problem/Ansatz: ist das so richtig ausgerechnet?

Text erkannt:
3. Streckenlasten
Gegeben ist das folgende Regal.
Auf der linken Seite ist das Regal fest aufgelagert an der Wand befestigt (A).
Zudem hängt das Bücherregal an einer Aufhängung, an einer Schiene an der Decke, an der die Aufhängung sich verschieben lässt. Diese Aufhängung hält einer maximalen Belastung von 200 N stand.
Auf dem Regal steht links die Blumenvase von \( 1,8 \mathrm{~kg} \) Masse.
Rechts daneben sollen ab 20 cm neben der Vase nach rechts Bücher aufgereint werden. Wir nehmen an, dass die Bücher im Durchschnitt 5 cm dick sind und 1kg Masse haben.
3.1 Wieviele Bücher können maximal auf dem Regal abgestellt werden, damit die Aufhängung der Belastung standhält?
3.2 Könnte man die Belastung erhöhen, wenn man die Aufhängung B nach rechts oder links verschieben würde?
\( \begin{array}{l} 11=20 \mathrm{~cm} \\ 12=20 \mathrm{~cm} \\ 13=30 \mathrm{~cm} \end{array} \)
6/9
Text erkannt:
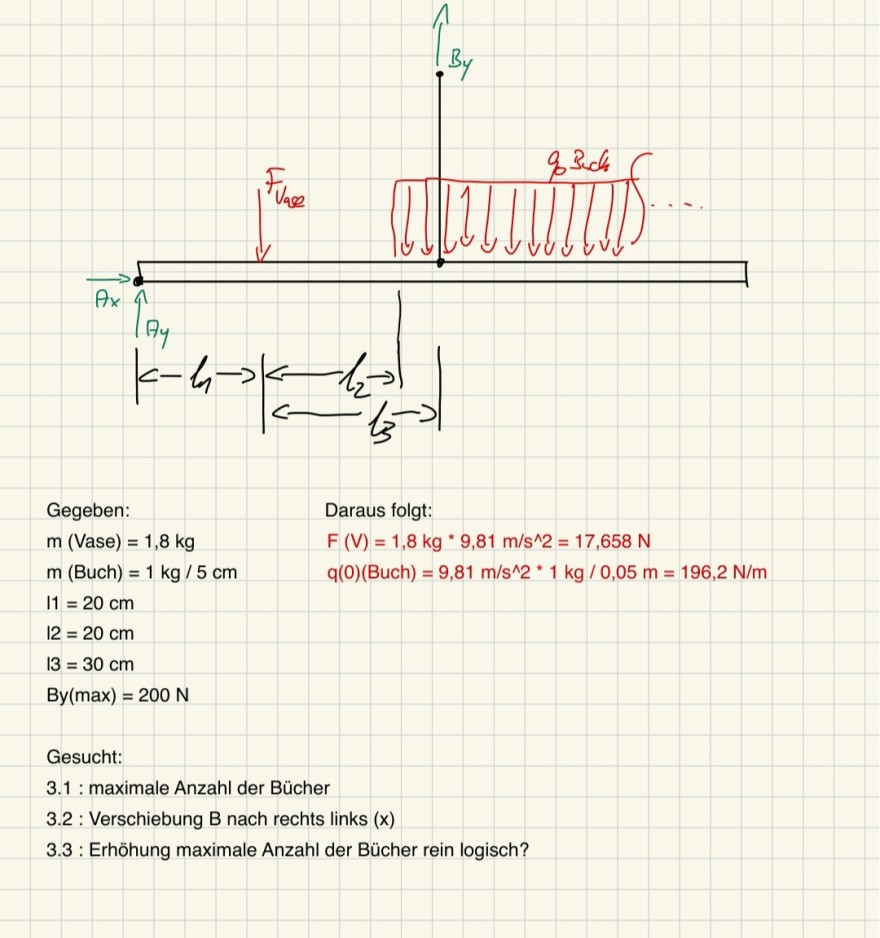
Gegeben:
\( \begin{array}{l} m(\text { Vase })=1,8 \mathrm{~kg} \\ m(\text { Buch })=1 \mathrm{~kg} / 5 \mathrm{~cm} \\ \mid 1=20 \mathrm{~cm} \\ \mid 2=20 \mathrm{~cm} \\ \mid 3=30 \mathrm{~cm} \\ \text { By }(\max )=200 \mathrm{~N} \end{array} \)
Daraus folgt:
\( \begin{array}{l} F(V)=1,8 \mathrm{~kg} *^{*} 9,81 \mathrm{~m} / \mathrm{s}^{\wedge} 2=17,658 \mathrm{~N} \\ q(0)(\text { Buch })=9,81 \mathrm{~m} / \mathrm{s}^{\wedge} 2^{*} 1 \mathrm{~kg} / 0,05 \mathrm{~m}=196,2 \mathrm{~N} / \mathrm{m} \end{array} \)
Gesucht:
3.1 : maximale Anzahl der Bücher
3.2 : Verschiebung B nach rechts links ( x )
3.3 : Erhöhung maximale Anzahl der Bücher rein logisch?

Text erkannt:
\( \begin{array}{l} \text { Geg. } \\ \text { I: } \sum F_{x}=0=A_{x} \\ \text { II: } \sum F_{y}=0=A_{y}+B_{y}-F_{v}-90 B_{B} \cdot x \\ \sum M_{A}=0=B_{y} \cdot\left(l_{1}+l_{3}\right)-F_{V} \cdot l_{1}-q_{0} \cdot x \cdot\left(l_{1}+l_{2}+\frac{x}{2}\right) \\ 0=96,4684 \mathrm{Nm}-196,\left.2 \frac{\mathrm{~N}}{\mathrm{~m}} \times\left(0,4 \mathrm{~m}+\frac{x}{2}\right) \quad \right\rvert\,:-196,2 \frac{\mathrm{U}}{\mathrm{~m}} \\ 0=x\left(0,4 m+\frac{x}{2}\right)-0,491683995 m^{2} \quad \mid .2 \\ 0=x^{2}+0,8 m x-0,983367991 m^{2} \\ x_{1 / 2}=-0,4 \mathrm{~m}=\sqrt{(0,4 \mathrm{~m})^{2}+0,983367991 \mathrm{~m}^{2}} \\ =-0,4 \mathrm{~m} \pm 1,0693 \mathrm{~m} \\ x_{1}=-1,4693 \mathrm{~m} \quad x_{2}=0,6693 \mathrm{~m} \\ \text { per Aufgabenstellung } \\ \text { nach rechls, heipt } \\ Y \text { in } F_{B}=90 B \cdot x=135,97 \mathrm{~V} \\ x=66,93 \mathrm{~cm} \\ \text { Anzahl } n=\frac{x}{5 \mathrm{am} / \mathrm{n}}=13,386 \\ \text { =13 Biclies } \\ \text { Lösung 3. } 1 \\ x \text { in II } \quad B_{y}=901 \cdot x+F_{v} \cdot B_{y}=-51,02534 \mathrm{~N} \end{array} \)
\( 3.21 \)
Was bedeutet \( \mathrm{Ay}= \) negativ?
Derzeit zieht das feste Lager A das Regalbrett nach untern bei gegebener Last Bücher. Diese Last kommt auch vollständig auf die Aufhängung B.
Allein durch die Reduktion dessen könnte man die Anzahl Bücher erhöhen.
