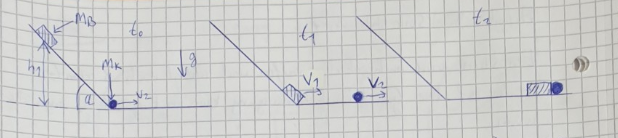
Zum Zeitpunkt \( t_{0}=0 \) befindet sich ein Block (Masse \( m_{B} \) ) in Ruhe am oberen Ende einer Rampe der Höhe h1 und der Neigung a \( =45° \). Zum selben Zeitpunkt befindet sich am unteren Ende der Rampe eine Kugel ( Masse \( m_{k} \) , Radius \( r_{k} \) , Trägheitsmoment 2/5 \( m_{k}r^2k \) ) mit der Geschwindigkeit v2. Jetzt beginnt der Block in einer konstanten beschleunigten Bewegung der Rampe hinunter zu rutschen, so dass er zum Zeitpunkt t1 die Geschwindigkeit v1 am Ende der Rampe erreicht hat. Während dieser Zeitspanne bewegt sich die Kugel mit der Konstanten Geschwindigkeit v2 vorwärts. Sobald der Block am unteren Ende der Rampe angekommen ist, bewegt er sich ebenfalls mit konstanter Geschwindigkeit v1 vorwärts.
Da \( v_{1}=2 \mathrm{v}_{2} \) ist, kommt es zu einem Zeitpunkt t2 zu einem teil elastischen Stoß zwischen den Körpern. Die Stoßzahl beträgt \( e=\frac{1}{2} \). Alle beschriebenen Vorgänge sind Reibungsfrei und beide Körper können für die Rechnungen ( abgesehen von Aufgaben-bild) als Punktmassen angenommen werden.
a) Welche Geschwindigkeit hat der Block am Ende de Rampe?
b) Nach welcher Zeit tges treffen die beiden Körper aufeinander?
c)Berechnen Sie die Geschwindigkeiten von Kugel und Block nach den Stoß.
d) Wenn die Kugel nach den Stoß ins Rollen übergeht, wie ändert sich die Geschwindigkeit?
$$ h_{1}, a=45° , m_{B}, m_{k}=4 m_{B}, v_{2}=\frac{1}{2} v_{1}, g $$
hinweif: \( \sin \left(45^{\circ}\right)=\frac{1}{\sqrt{2}}=\cos \left(45^{\circ}\right) \)

Habe ich a) überhaupt richtig so?
die Berechnung hatte ich gestern schon oben aufgeschrieben in Klartext!
Gruß