Hallo Tekto,
verlasse Dich nicht zu sehr auf mich. Zum einen bin ich nicht ständig online - Ende August werde ich zwei Wochen off sein - und zum anderen sind viele TM-Aufgaben i.A. relativ umfangreich zu beantworten (für diese gilt das nicht). Heißt: ich muss mir dazu extra Zeit nehmen, das kann ich nicht eben so zwischen durch machen, wie viele der Mathe(Haus-)Aufgaben.
Wie gehe ich hier vor, muss ich wieder ganz normal schneiden und die Querkräfte, Normalkräfte, sowie das Moment bestimmen?
Ja genau, und ich gehe davon aus, dass Du das inzwischen kannst. Hier noch mal eine Skizze, wie ich Deine Skizze verstanden habe:
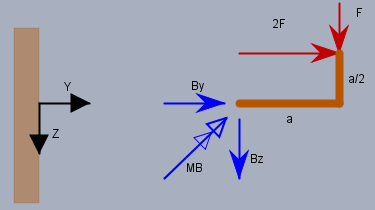
Die Schnittgrößen (blau), die auf das rechte Stück wirken, sind relevant für die Spannungen. Sie sind: $$ \begin{aligned} B_y&= -2F \\ B_z& = -F \\ M_B&\cancel{= -3aF} = -\frac{a}{2} \cdot 2F - a \cdot F = -2aF \end{aligned}$$ Die Vorzeichen spielen jetzt nur in soweit eine Rolle, dass man sich darüber klar werden muss, wo Zug- und wo Druckspannungen herrschen. Im folgenden ignoriere ich formal die Vorzeichen. Massgeblich sind bei Biegebalken i.A. nur die Biege- und Zugspannungen. Die werden zunächst gesondert bestimmt. \(M_B\lt 0\) d.h. für diesen Balken, dass oben Zug- und unten Druckspannungen vorliegen. Es ist:
$$\sigma_{\max} = \frac{M_B}{W_x}$$ (siehe auch Widerstandsmoment) und $$W_x = \frac{I_x}{a_{\max}}$$ wobei \(a_{max}\) der maximale Abstand des Materials von der neutralen Faser ist. Hier ist $$a_{\max} = \frac12 h$$ also
$$W_x = \frac{I_x}{a_{\max}} = \frac{\frac{1}{12}b h^3}{\frac12 h} = \frac{1}{6} b h^2$$ was sich mit der Gleichung für einen rechteckigen Querschnitt deckt, die Du hinter dem Link findest. Die maximale Spannung ist demnach
$$\sigma_{\max} = \frac{M_B}{W_x} = \frac{6 \cdot 2aF}{ bh^2}= \frac{12 \cdot 20\text{mm} \cdot 10\text{N}}{20\text{mm} \cdot \left( 10 \text{mm}\right)^2} = 1,2 \frac{\text{N}}{\text{mm}^2}$$
Die Zugspannung ist
$$\sigma_{\text{zug}} = \frac{B_y}{hb} = \frac{2 \cdot 10\text{N}}{10 \text{mm} \cdot 20 \text{mm}} = 0,1 \frac{\text{N}}{\text{mm}^2}$$ Die Zugspannung addiert sich im Zugbereich (also oben im Balken) zu der Biegespannung hinzu und hebt im Druckbereich (unten) diese teilweise auf. Somit ist
$$\begin{aligned} |\sigma_{oben}| &= 1,3 \frac{\text{N}}{\text{mm}^2} \\ | \sigma_{unten}|&= 1,1 \frac{\text{N}}{\text{mm}^2}\end{aligned}$$
Ich habe jetzt ganz bewusst Betragsstriche hinzugefügt, und mir damit die Sache mit dem Vorzeichen leicht gemacht. Keine Ahnung, ob Ihr Zug- oder Druckspannung als positiv definiert. Weiter ist Dir sicher aufgefallen, dass ich die Schubspannung ignoriert habe. Wenn Du diese hinzurechnest, musst Du Dich mit dem Spannungstensor auseinander setzen. Bei Biegebalken braucht man das i.A. in der Praxis nicht, da die Biegespannungen konstruktionsbestimmend sind.
Gruß Werner