Kraft F sowie Auflagerreaktion A bestimmen, in einer Walze, wie gehe ich am besten vor?

Question

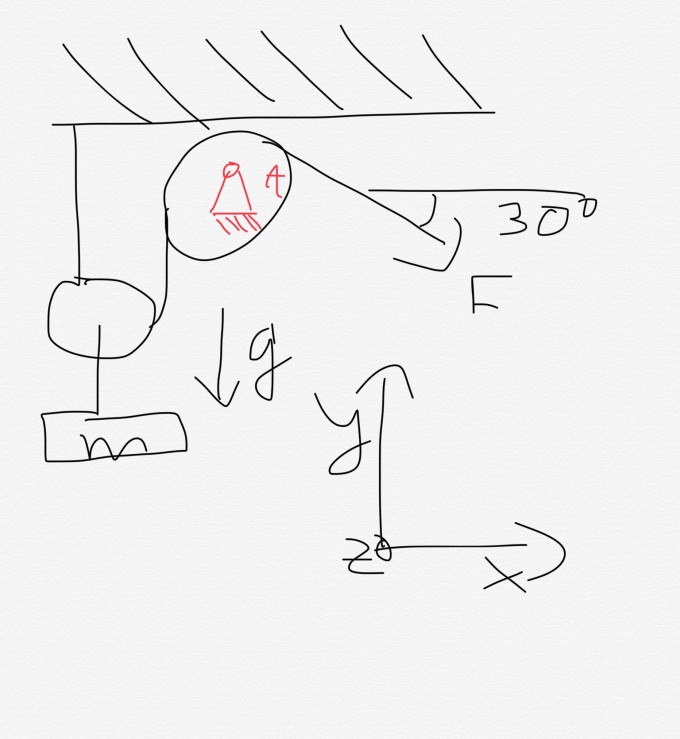
Hallo Leute,

kann mir vielleicht jemand bei dieser Aufgabe weiter helfen. Ich weiß echt nicht, wie man diese Aufgabe lösen kann. Ich kann höchstens F in ihre X und Y Komponente zerlegen, danach weiß ich leider nicht mehr weiter, was ich mit den Walzen anfangen soll.

Ich habe m und g gegeben.

ich gehe jetzt mal davon aus, das g, die Gewichtskraft darstellen soll.

Ich habe zwei Walzen, in der eine Walze mit der Masse 'm' verbunden ist, allerdings weiß ich nicht wie groß diese ist.

In der anderen Walze ist eine Auflagekraft A drinnen.

Ich soll F berechnen, sowie A.

Ich würde F*cos30, sowie F*sin30 berechnen, aber danach weiß ich nicht mehr weiter. Wie soll man hier etwas berechnen?

Ich bin jedem für seine Hilfe dankbar.

LG Marco

Answer 1

Hallo Marco,

für die Position des Punktes \(A\) gibt es keine Angaben. Daher nehme ich an, dass die Seilabschnitte, die von der beweglichen Rolle ausgehen, senkrecht verlaufen. Es gelten i.A. die üblichen Annahmen von masselosen und reibungsfreien Rollen. Dann ist die Seilkraft $$F = \frac12 m\cdot g$$ die halbe Gewichtskraft (simpler Flaschenzug mit einer Rolle).

Die Kraft \(\vec{A}\), die auf das Lager \(A\) wirkt, ist schlicht die Summe der beiden Seilkräfte:

$$\vec{A} = F \cdot \begin{pmatrix} 0 \\ -1\end{pmatrix} + F \cdot \begin{pmatrix} \cos 30° \\ -\sin 30°\end{pmatrix}$$ die Y-Koordinate ist negativ, da sie nach unten zeigt.

Alles klar?

Gruß Werner

Comments

Danke Werner,

Aber wieso ist F= 1/2 m* g?

Also wenn ich richtig verstanden habe hat das was mit den Seilen und walzen zu tuen? Hätte ich jetzt beispielsweise statt zwei Walzen, drei Walzen wäre dann F= 1/3 m* g oder wie sieht das aus ?

Und zu der Auflagereaktion, muss ich diesen nicht freischneiden? Weil würde ich die Kraft schneiden hätte ich doch glaub ich eine vertikale und horizontale Kraft ?

---

Natürlich Gruß Marco ;-)

---

Hallo Marco,

Also wenn ich richtig verstanden habe hat das was mit den Seilen und walzen zu tuen?

es hat nur was damit zu tun, wie viele Seilabschnitte das Gewicht tragen. In Deinem Fall sind es zwei.

So wären es drei:

dabei ist es völlig egal, ob das Seil hinter \(F/3\) noch über irgendwelche Rollen geführt wird oder nicht.

Weil würde ich die Kraft schneiden hätte ich doch glaub ich eine vertikale und horizontale Kraft ?

hast Du doch schon! Vertikal \(F(-1-\sin 30°)\) und horizontal \(F \cdot \cos 30°\) - steht da doch - oder?.

Falls noch was unklar ist, so frag' ruhig.

Gruß Werner

---

Achso jetzt verstehe, es hängt wirklich tatsächlich von den Seilsbschnitten ab, anhand dessen kann ich dann also die Kraft bestimmen. Ich habe mal zur Beispielzwecken eine Skizze rein gepackt. Wenn ich jetzt wirklich alle Seile penibel abzählen würde , hätte ich insgesamt 4 Seilabschnitte, richtig? Die Seile die in die Wälze mit reingehen zähle ich nicht mit oder ? Wenn ich diese mitzählen würde, hätte ich ja insgesamt 6 Seile dann müsste laut das F=m*g/6 sein oder ?

Ist hier F= m*g/ 4? 

PS: kennst du dich mit Schnittgrößenverläufen auch aus? Bzw Balken

Lg Marco

---

Ich habe es mir noch mal angeguckt, es müsste eigentlich heißen F= m*g/8, weil jede Seilkraft müsste ich ja mal 1/2 nehmen. Bei der Zweiten Walze wären es F=m*g/4 und bei der letzten F´=m*g/8. Da ich hier für F keinen Winkel gegeben habe, belasse ich es auch hierbei

---

Hallo Marco,

Bei der Zweiten Walze wären es F=m*g/4 und bei der letzten F´=m*g/8.

Die dritte Walze tut nichts zur Sache. Sie lenkt nur das Seil um. Du hast es hier mit zwei Seilen zu tun, in denen eine unterschiedliche Seilkraft vorliegt.

Wichtig ist:

1.) Die Summe aller Kräfte an einem geschlossenen System ist gleich Null.

2.) innerhalb eines(!) Seils bleibt die Seilkraft konstant (Reibungsfreiheit vorausgesetzt)

 

Damit kann man bei einer einfachen Rolle sofort sagen, wie sich die Kräfte an Seil und Rolle untereinander verhalten. Da sie Seilkraft an einem Seil überall gleich ist, sind die beiden Kräfte, die nach oben wirken, identisch. Und da die Summe aller Kräfte =0 ist, muss $$F = 2S$$ sein. Zumindest was den Betrag angeht. Die Kräfte wirken in die Richtungen, wie ich sie eingezeichnet habe.

Jetzt schneide ich bei dem Flaschenzug aus Deinem letzten Kommentar mal die einzelnen Rollen frei.

Die Seilkraft im grünen Seil sei \(S_b\) . Wenn man mit 'Schnitt 1' die untere Rolle frei schneidet, dann ist klar: $$S_b = \frac12 G$$ Die Seilkraft im schwarzen Seil sei \(F\). Schneidet man in 'Schnitt 2' frei, so sieht man $$S_b + F + F = G \quad F = \frac12(G - S_b) = \frac14 G$$ Die dritte Rolle rechts oben teilt keine Kraft mehr auf. Es bleibt dabei $$F = \frac14 G = \frac14 m\cdot g$$ Gruß Werner

---

Hallo Werner,

Kannst du mir bitte noch mal sagen, wie du die Lagerkraft A berechnet hast?

Also ich verstehe nicht, wie du bei A die Annahme machen konntest das A= F*(0 in x und in y -1) machen konntest.  Ay geht doch nach oben, da y nach oben positiv ist, ist es doch dann positiv 1? Und Ax müsste doch nach rechts gehen also +1 in x?

---

Hallo Tekto,

ich schrieb:

Die Kraft \(\vec{A}\) , die auf das Lager A wirkt, ...

und diese Kraft wird in diesem Fall ausschließlich durch die Seile hervorgerufen. Der eine Seilabschnitt zieht senkrecht nach unten (negative Y-Richtung), der andere unter einem Winkel von \(30°\) nach rechts unten (positive X- und negative Y-Richtung).

Im Allgemeinen bezeichnet man mit 'Lagerkraft' die Kraft, die das Lager auf die Konstruktion ausübt (hier auf die Rolle). Ist die Lagerkraft im Lager \(A\) gleich \(\vec{L}_A\), so wäre hier \(\vec{L}_A = -\vec{A}\).

Gruß Werner

PS.: ich kümmere mich jetzt um Deine aktuelle offene Frage.

---

Hallo Werner,

ich danke dir vielmals.

Und natürlich schon mal jetzt Danke, für die Klärung der offenen Frage! Bei der stehe ich auf dem Schlauch.

Lg Tekto