Physik: Wie komme ich auf die Umformung der Beschleunigung?

Question

Aufgabe:

Beschleunigung: Wie viele Meter pro Sekunde werde ich in einer Sekunde schneller?

\( \vec{a}=\frac{d}{d t}\left(\frac{d \vec{s}}{d t}\right)=\frac{d^{2} \vec{s}}{d t^{2}} \)

Es geht um diese generelle Formel der Beschleunigung: Wie komme ich darauf? Mich verwirren auch die Deltas in der Formel.

Answer 1

Hallo,

Im Grunde ist dies die Definition der Beschleunigung. Man ist also nicht drauf gekommen im Sinne einer Berechnung, sondern man hat gemerkt, dass die zweite Ableitung nach der Position \(\vec{s}\) eine sinnvolle Größe ist, die man Beschleunigung nennt.

Vor der Beschleunigung hat man Geschwindigkeit definiert. Geschwindigkeit ist die erste Ableitung von \(\vec{s}\) nach der Zeit.

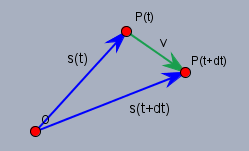
Stelle Sir vor, Du befindest Dich zum Zeitpunkt \(t\) z.B. mit einem Fahrrad an der Position \(\vec{s}(t)\). Und Du fährst mit dem Fahrrad. Schaut man nun einen sehr kleinen Zeitraum \(\Delta t\) in die Zukunft, so bist Du und das Fahrrad nicht mehr bei \(\vec{s}(t)\) sondern bei \(\vec{s}(t + \Delta t)\). Und genau wie beim Differenzieren einer Funktion (was anderes ist das hier auch nicht!) bestimmt man nun die Geschwindigkeit \(\vec{v}\) aus:

$$\vec{v} = \frac{\text{d} \vec{s}}{\text{d}t}= \lim_{\Delta t \to 0} \frac{\vec{s}(t + \Delta t) - \vec{s}(t)}{\Delta t}$$

Genauso geht es mit der Beschleunigung weiter. Hier wird wieder nach der Zeit differenziert.

$$\vec{a} = \frac{\text{d} \vec{v}}{\text{d} t} = \frac{\text{d} }{\text{d} t} \left( \frac{\text{d} \vec{s}}{\text{d}t} \right) = \frac{\text{d}^2 \vec{s}}{\text{d}t^2}$$Und das mit den \(\text{d}\)'s bzw. deltas ist einfach nur eine Schreibweise. Falls irgendwas unklar ist, so frage bitte noch mal nach.

Gruß Werner

Answer 2

Vielleicht ein etwas einfacherer
Erklärungsversuch.
Die einfachste Bewegung ist die gleichförmige
Bewegung. Versuch : Metallkugel über
eine Glasplatte rollen lassen und Weg und Zeit
messen.

Mathematisch ist v = s / t.
v = s ´oder die erste Ableitung von s.
v ist konstant.

Die zweite Bewegung ist die gleichförmig beschleunigte
Bewegung. Versuch : einen Körper frei falllen lassen
und den Weg und die Zeit messen.

Die erste Ableitung ist die Geschwindigkeit.
Die Geschwindigkeit nimm linear zu.
Die 2.Ableitung wird Bescheunigung genannt und
ist konstant.
Integegriert man so erhält man
a ( konstant )
v = a * t
s = ∫ a * t dt
s = 1/2 * a * t^2

Answer 3

Mach dir erst mal klar, was die Geschwindigkeit ist:

Die momentane Änderungsrate der Wegfunktion also

die Ableitung der Wegfunktion nach der Zeit, also v = s ' (t) oder

ds/dt  oder d/dt ( s) 

Und die Beschleunigung ist die momentane Änderungsrate der

Geschwindigkeitsfunktion also die Ableitung der

Geschwindigkeitsfunktion nach der Zeit, also  a =  v ' (t) oder

dv/dt  = d/dt (v) = d/dt ( ds/dt)  = d² s / dt²