Hallo liebe Mathefreunde,
ich sitze gerade vor einer Statikaufgabe, bei der ich einen Winkel bestimmen muss.
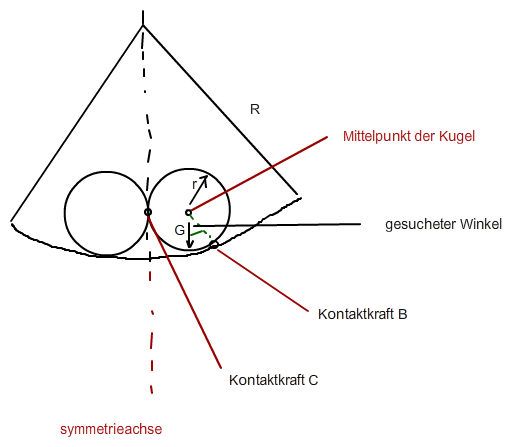
Gegebene Daten: R=120 mm , r =40 mm
ich bräuchte nur einen Tipp für die Winkelbeziehungen in diesem Falle, also wie ich den gesuchten Winkel ausrechnen kann..
Falls sich jemand genauer mit dem Thema beschäftigt:
Meine Gleichgewichtsbedingungen (statisch):
$$\sum { { F }_{ x }=0=C+B*sin(\alpha ) } \\ \\ \sum { { F }_{ y }=0=-G-B*cos(\alpha ) }$$
(Habe das System in der Zeichnung schon "halbiert" wegen der Symmetrie!)
Vielen Dank im Voraus !!!