Vom Duplikat:
Titel: Auflagekräfte berechnen aber wie?
Stichworte: kraft,tangens,mechanik
Hey,
Ich lerne gerade für ne wichtige Prüfung. Ich weiss leider nicht wie ich auf die Auflagekräfte komme... wie kommen die in der Lösung auf tan bei Ay, By, S?
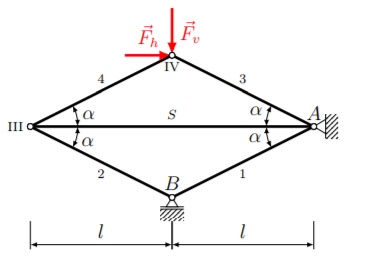
Aufgabe: Der dargestellte Scherenwagenheber wird durch eine horizontale Kraft FH und eine vertikale Kraft FV belastet.
Gegeben: FH, FV, l, α
Gesucht: sind die Auflagekräfte A und B und die Stabkraft S in der Gewindespindel.
Lösung: Ax= -F, Ay= FH tan(α), Bx= 0, By= FV - FH tan(α) , S= B* cot(α)