Hallo,
alternativ zu der Berechnung oben gibt es noch eine andere Möglichkeit die Spannung am Verbraucherwiderstand RV zu berechnen.
Vorher aber noch ein Hinweis:
In der Berechnung oben hat sich eine kleine Verwechslung eingeschlichen. Das Bild zeigt den Zusammenhang von Kabelwiderstand RK und der Hilfsvariablen Z, also nicht von Verbraucherspannung URV und Hilfsvariablen Z. Deshalb ist der Satz über dem Bild "Der Graph dieser Funktion zeigt das Bild" falsch.
Hier nun der alternative Rechenweg zur Bestimmung der Verbraucherspannung URV .
Ausgegangen wird wieder von den folgenden beiden Gleichungen
Gleichung 1: URK = RK • URV / RV
Gleichung 2: URK = 230V − URV
RK Kabelwiderstand
RV Verbraucherwiderstand
URK Spannung über dem Kabelwiderstand
URV Spannung über dem Verbraucherwiderstand
Durch Gleichsetzen von URK aus Gleichung 1 und Gleichung 2 und auflösen nach URV erhält man Gleichung 3:
Gleichung 3: URV = 230V • RV /RK − URV • RV /RK
Die Leistung im Verbraucherwiderstand errechnet sich zu
PRV = U2RV /RV diese Formel umgestellt nach RV
RV = U2RV / PRV setzt man RV in Gleichung 3 ein, erhält man Gleichung 4
Gleichung 4: URV = 230V • (U2RV / PRV) / RK − URV • (U2RV / PRV ) / RV
Löst man diese Gleichung nach URV auf und setzt für PRV den Wert von 100W ein, erhält man Gleichung 5:
Gleichung 5: URV = 115V − ✓¯(115V2 − 100W • RK )
Hinweis: das Wurzelzeichen geht über die Klammer hinweg.
Diese Gleichung beschreibt den Zusammenhang von Verbraucherspannung URV in Abhängigkeit vom Kabelwiderstand RK . Der Graph dieser Funktion zeigt das Bild.
Verbraucherspanng URV als Funktion von Kabelwiderstand RK .
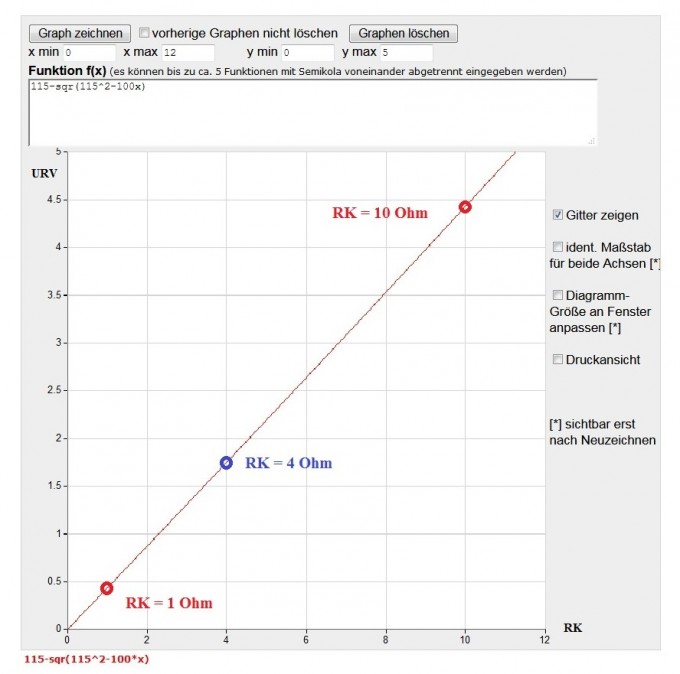
Rot eingezeichnet sind Werte für Kabelwiderstände 1Ω und 10Ω. Zusätzlich ist als Beispiel ist die Verbraucherspannung bei einem Kabelwiderstand von 4Ω.
Hier die Werte:
bei RK = 1Ω beträgt URV = 0,436V
bei RK = 4Ω beträgt URV = 1,752V
bei RK = 10Ω beträgt URV = 4,433V
Auf den ersten Blick scheint diese Kennlinie eine Gerade zu sein. Tatsächlich handelt es sich um ein Wurzelfunktion. Man kann das überprüfen, indem man in Gleichung 5 für RK Werte zwischen 50Ω und 100Ω einsetzt und URV ausrechnet. Die Krümmung der Kurve ist dann deutlich zu erkennen.
Gruß von hightech