Hallo equinox,
Erster Schritt: mache eine Zeichnung (s.u.). Zeichne eine Koordinatensystem ein - hier \(e_1\), \(e_2\) und \(e_3\). Trage die interessierenden Kräfte ein. Zeichne die bekannten Kräfte in die Richtung, in die sie auf das frei geschnittene Tragwerk wirken und die unbekannten Kräfte und Momente in Richtung der Koordinatenachsen (wenn positives Schnittufer).
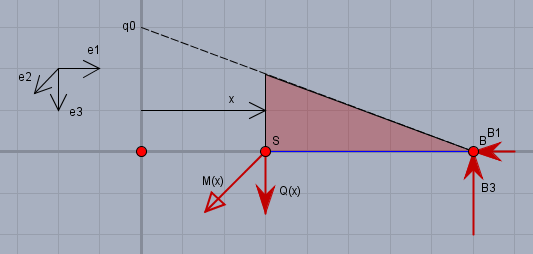
Mein Tool kann keine Teilkreise. Der Pfeil schräg beim Schnittpunkt \(S\) mit der offenen Spitze, soll das Moment \(M_2(x)\) sein. Das Moment \(M_2\) kommt aus der Zeichenebene heraus in Richtung der \(e_2\)-Achse. Die Kräfte im Lager \(B\) sind gegeben. Da sie beide negativ sind, trage ich sie entgegen der Koordinatenrichtungen ein. Die Momentensumme um \(S\) gibt nun:
$$M_2(\bar x_1) + (l- \bar x_1)B_3 - \int_{\bar x_1}^l (x-\bar x_1) q(x) \space \text{d}x = 0$$
Die Streckenlast \(q(x)\) ist: \(q(x) = q_0 - (q_0/l) x\). Oben Einsetzen und Auflösen nach \(M_2(\bar x_1)\) gibt $$\begin{aligned}M_2(\bar x_1) &=\int_{\bar x_1}^l (x-\bar x_1) (q_0 - \frac{q_0}{l} x) \space \text{d}x - (l- \bar x_1)B_3 \\ &=\int_{\bar x_1}^l \left( x(q_0 + \bar x_1 \frac{q_0}{l}) - \frac{q_0}{l}x^2 - \bar x_1 q_0 \right) \space \text{d}x - (l- \bar x_1)B_3 \\ &= \left. \frac12 x^2 (q_0 + \bar x_1 \frac{q_0}{l}) - \frac13 \frac{q_0}{l} x^3 - \bar x_1 q_0 x \right|_{\bar x_1}^l - (l- \bar x_1)B_3 \\ &= \frac12 (l^2 - \bar x_1^2) (q_0 + \bar x_1 \frac{q_0}{l}) - \frac13 \frac{q_0}{l}(l^3 - \bar x_1^3) - \bar x_1 q_0 (l - \bar x_1) - (l- \bar x_1)B_3 \\ &= \frac{-1}{6} \frac{q_0}{l} \bar x_1^3 + \frac12 q_0 \bar x_1^2 + ( B_3 - \frac12 q_0 l)\bar x_1 + \frac16 l^2 q_0 - l B_3 \\ &= \frac{-1}{10} \frac{\text{N}}{\text{m}^2} \bar x_1^3 + 15 \frac{\text{N}}{\text{m}}\bar x_1^2 - 270 \text{N} \bar x_1 - 11500 \text{Nm} \end{aligned}$$
was der obigen Lösung entspricht exklusiv des Vorzeichens, was IMHO aber nur Sache der Definition ist. Für die Lösung wurde hier anscheinend ein negatives Schnittufer angenommen. Die Querkraft ist jetzt einfach die Ableitung des Moments nach dem Ort \(\bar x_1\).
Gruß Werner