Hallo liebe community,
mit der Bitte um Kontrolle.
Fragestellung:"Beim schiefen Wurf ohne Reibung wird die größte Wurfweite bei einem Winkel von 45°erzielt. Ist das auch beim Kugelstossen so? Berechnen sie die jeweilige Wurfweite die sich ergibt, wenn der Athlet die Kugel in einer Höhe von 1,65m mit einer Geschwindigkeit von 14m/s unter einem Winkel von 45° und 43° losschleudert."
Ich hab nun eine Skizze angefertigt und den Wurf in zwei Phasen eingeteilt. Abwurf p1 bis p2 im schiefen Wurf ohne Reibung, und waagrechter Wurf ohne Reibung von p2 bis p3.
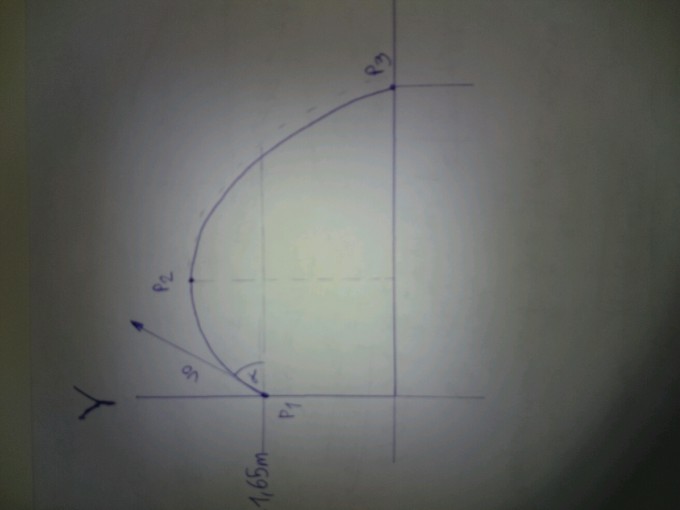
1.) 45°
Es ergibt sich eine Flugzeit von p1 nach p2 von 1,01s, daraus resultierend eine zusätzliche höhe Y von 5m mit einer Wurfweite X von 9,998m.
Die Flugzeit von p2 nach p3 beträgt 1,164s mit da die Höhe des Wurfes 5m und die Abwurfhöhe von 1,65m addiert wird. Ich erhalte für diesen Abschnitt eine Wurfweite von 11,526m.
Kumulierte Wurfweite p1+p2+p3=21,524m
2.) 43°
Es ergibt sich eine Flugzeit von p1 nach p2 von 0,973s, daraus resultierend eine zusätzliche höhe Y von 4,643m mit einer Wurfweite X von 9,961m.
Die Flugzeit von p2 nach p3 beträgt 1,132s mit da die Höhe des Wurfes 4,643m und die Abwurfhöhe von 1,65m addiert wird. Ich erhalte für diesen Abschnitt eine Wurfweite von 11,596m.
Kumulierte Wurfweite p1+p2+p3=21,557m
Lösung: Die Wurfweite ohne Reibung bei 43°ist geringfügig höher als bei 45°.
Danke für eure Rechenkünste im Vorhinein!!!
Liebe Grüße,
elrippo