Hallo Mistermathe! :-)
Bogen
\( \sin(45°) = \cos(45°) = \frac{\sqrt2}{2} \)
\( y_s = \frac{2r^2 \sin(\alpha)}{b} \) https://de.wikipedia.org/wiki/Geometrischer_Schwerpunkt#Kreisbogen
Der Bogen ist ein Viertelkreis, ein Viertel des Umfangs:
\( b = \frac{U}{4} = \frac{2r \pi }{4} = \frac{1}{2}r\pi \)
Eingesetzt in y_s:
\( y_s = \frac{2r^2 \sin(45^{\circ})}{b} = \frac{2r^2 \sin(45^{\circ})\cdot4}{2r\pi} = \frac{r \sin(45^{\circ})\cdot 4}{\pi} = \frac{r \sqrt{2}\cdot4}{\pi\cdot 2}= \frac{2\sqrt{2}\cdot r}{\pi} \)
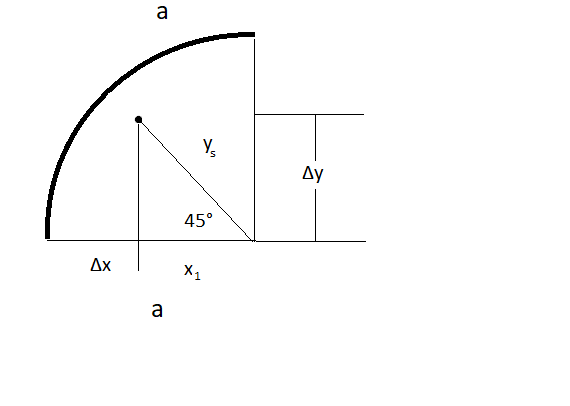
(Für die nächste Rechnung siehe Skizze)
\( \Delta y = y_s \sin(45^{\circ}) = y_s\frac{\sqrt2}{2} = \frac{2 \sqrt{2}\cdot r}{\pi}\frac{\sqrt{2}}{2} = \frac{2r}{\pi} \)
\( x_1 = y_s\cos(45°) = \frac{2\sqrt{2}\cdot r}{\pi} \frac{\sqrt{2}}{2} = \frac{2r}{\pi} \)
\( \Delta x = r- x_1 = r - \frac{2r}{\pi} \)
Wenn Du r=a setzt, kommst Du auf die Werte der Lösungshilfe.
Nachtrag:
$$ y_2 = 8a + \Delta y = 8a + \frac{2r}{\pi} = 8a + \frac{2a}{\pi} = 8m + \frac{2m}{\pi} = 8.64m \\x_2 = \Delta x = r - \frac{2r}{\pi} = a - \frac{2a}{\pi} = 1m - \frac{2m}{\pi} = 0.36m $$
Masse
Einfach die Länge des Viertelkreises mit mR multiplizieren.
Nachtrag: \( m_2 = b\cdot m_R=\frac{1}{2}r \cdot \pi\cdot m_R = \frac{1}{2}a \cdot \pi\cdot m_R = \frac{1}{2}\cdot 1m \cdot \pi\cdot 10\frac {kg }{ m } = 15.71kg \)
Das war gerade hopp hop hopp... hoffe, dass nicht so viele Fehler drin sind, bin gerade kurz angebunden, kann also nicht viel erklären. Falls Du noch Fragen hast, nur zu, ich bin morgen wieder online.
Beste Grüße
gorgar