Resultierende Seilkraft bei horizontaler Krafteinwirkung

Question

Hallo zusammen,

kann mir jemand bei dieser Aufgabe helfen?
Ich komme nicht wirklich voran da ich mich durch die Überlegung auf den Winkel Alpha zu schließen etwas blockiere ..
Kann mir jemand helfen? - vielen Dank.

Comments

Satz des Pythagoras

1^2 + h^2 = (2 - h)^2 --> h = 3/4

tan(α) = 1/ (3/4) --> α = 53.13°

Answer 1

α = 53.13°

F ( verti ) = 1
tan ( a ) = F ( hori ) / 1

sin ( a ) = F ( hori ) / F ( seil )

mfg Georg

Comments

Gern geschehen.

---

Ein gespanntes Seil kann nur eine Kraft in Richtung des Seils aufnehmen, daher verläuft die Wirkungslinie der Kraft S (Resultierende von G und H) in Richtung des diagonalen Seils, siehe Bild von Georg.  Das *senkrechte* Seilstück übt keine Kraft aus.

---

Hallo Georg, in deiner Lösung ist die Kraft auf das senkrechte Seilstück null.  Kann das sein?  Siehe Bild.  Hier ist F2 ungleich null.

---

Wäre es möglich, dass mir jemand noch eine Lösungsweg skizziert? - ich komme einfach nicht weiter ..

---

@mrmath
1.Frage ist die Herleitung des Winkels klar ?

@Roman
In beiden Seilen herrschen Zugkräfte.
Ein Seil kann nur Zug aufnehmen.
In meiner Skizze habe ich den Pfeilspitze 
senkrecht nach unten vergessen.
Meinst du das ?

mfg Georg

---

Ja, der Winkel ist soweit klar.

---

Hallo Roman,

nehmen wir einmal an eine Kraft von 1.662 N
kommt unter dem Winkel von 53 ° an einem
Punkt an.
Dort wird die Kraft ersatzweise in einen horizontalen
und  einen vertkalen Teil aufgespalten

F ( horizontal ) = 1.327
F ( vertikal ) = 1

Die vertikale Kraft wird durch das
Gewicht von 1 N übernommen.

Nach rechts müßte mit 1.327 N
gezogen werden.

Meine Meinung.

---

Durch die Antwort konnte berechnet werden

α = 53.13°

F ( verti ) = 1 N
tan ( 53.13 ) = F ( hori ) / 1
F ( hori ) = 1.333 N

sin ( 53.13 ) = F ( hori ) / F ( seil )
sin ( 53.13 ) = 1.333 / F ( seil )
F ( seil ) = 1.666 N

---

F ( seil ) = 1.666 N   ist falsch.

Richtig ist  F_Seil = 625 N .

---

Hier die Zusammfassung aus den Diskussionen

Im Seil herrscht überall eine konstante Zugkraft
| F1 | = | F2 |

Der Winkel zwischen F1 und F2 beträgt 53.13°

An die Rolle greifen 4 Kräfte an.

Der Winkel der resultierenden Kraft aus F1 und F2
beträgt alpha = 53.13 / 2 = 26.565 °

G = 1 kN

tan ( a ) = H / G = H / 1 kN
H = 0.5 kN

Answer 2

Hallo mrmath, hier meine Skizze.  F ist die Winkelhalbierende von F1 und F2.  Dann ist nämlich Betrag(F1) = Betrag(F2), und die Rolle ist in Ruhe.  Ausführlicher, wenn ich mehr Zeit habe, oder ein Anderer ist schneller.

Comments

Hallo mrmath, auf die Rolle wirken 4 Kräfte:  Die Kräfte F1 und F2 in Richtung der beiden Seile sowie die Kräfte G und H aus der Aufgabe.  Es gilt F1 + F2 + G + H = 0, da die Rolle in Ruhe ist.  (Alles sind Vektoren.)  Zunächst bestimmen wir die Richtung der Kraft F = G + H.  F habe ich in meiner Skizze eingezeichnet.  Sie ist die Winkelhalbierende von F1 und F2 mit Betrag(F1) = Betrag(F2).  Wären F1 und F2 unterschiedlich groß, würde sich die Rolle in die eine oder andere Richtung bewegen. 

Der Winkel alpha, in der Aufgabe eingezeichnet, beträgt, wie an anderer Stelle schon geschrieben, 53,1 Grad.  Also schließt F mit der Vertikalen den Winkel 26,6 Grad ein.  Daraus berechnet man H = 1 kN * sin 26,6 Grad = 448 N und F = 1,10 kN.

---

Sorry:  H = 1 kN * tan 26,6 Grad = 501 N und F = 1,12 kN.

---

Eure ganze Winkelrechnerei ist doch völlig überflüssig.
Sie ist Quelle von Fehlern und Ungenauigkeiten.

Besser ist :

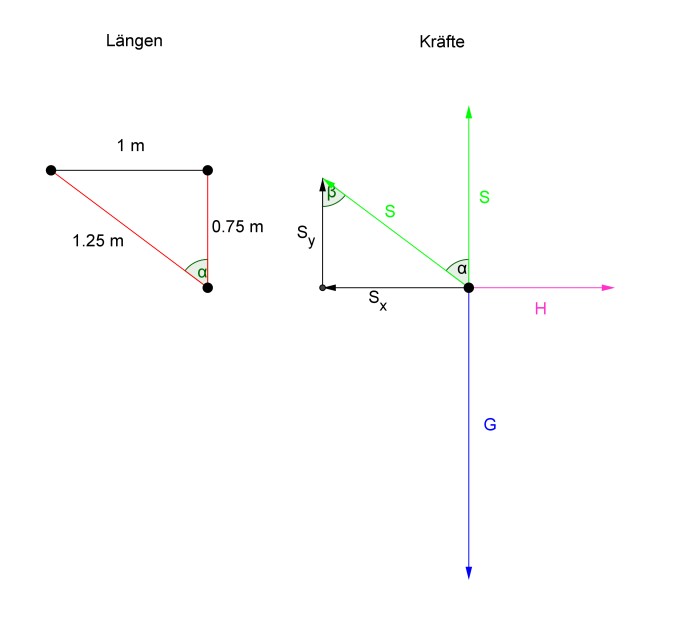
Im Folgenden werden nur die Beträge der Vektoren notiert, S ist die Spannung im Seil.

Wegen  α = β  sind die Dreiecke ähnlich und daraus folgt

einerseits
  S / 1,25  =  S_y / 0,75  und somit  S_y = 3/5 S
  und wegen  S_y + S  =  G  weiter  8/5 S  =  G
  also   S  =  5/8 G

und andererseits
  S / 1,25  =  S_x / 1  und somit  S_x  =  (5/8 G) / 1,25  =  0,5 G
  und wegen  S_x = H  also auch   H  =  1/2 G .

---

Hmm...  Ich würde gerne mal drüber nachdenken und diesen Kommentar hier löschen.  Aber man kann in Mathelounge zwar einen Kommentar bearbeiten, aber nicht zurücknemen.

---

Hallo hj2166, Hut ab, deine Rechnung ist eleganter.  Du hast die selbe Lösung wie ich, nur eben exakt und nicht gerundet.  :-)

---

Hallo Roman,

ich halte nichts davon Beiträge zu löschen.
Andere Mitleser können dann den Beitragsfaden
womöglich nicht mehr verstehen / nachvollziehen.

Im Forum nur richtige Beiträge eingestellt zu
haben hat bisher noch niemand geschafft.

Frage : im Seil ist überall dieselbe
Zugkraft vorhanden. Deshalb
| F1 | = | F2 | ?

---

Hallo Georg, ich hatte einen blöden Kommentar geschrieben und wollte den dann gleich wieder löschen.  Da das nicht geht, musste ich halt auf "Bearbeiten" klicken und Junk reinschreiben.

Korrekt.  Es gilt | F1 | = | F2 |.

---

Ersetze oder erweitere durch

" Kommentar wieder zurückgezogen "

---

Hallo Georg, ja, das ist eine gute Lösung.  Zur Aufgabe:  Wir haben eine Rolle.  Wäre in das Seil ein Angriffspunkt für G und H fest verankert, dann könnten die Kräfte F1 und F2 betragsmäßig unterschiedlich sein.  Aber nicht, wenn eine Rolle da ist, die sich auf dem Seil verschieben könnte.

---

Nachfrage : fiel mir noch vor deinem Kommentar ein.

Wenn es starre Träger wären dann wäre meine
Lösung zutreffend ?

---

Hallo Georg, deine Lösung war der „rechteste“ Pfeil in der oberen Gafik 1.  Da wirkt auf das rechte Seil überhaupt keine Kraft, nur auf das linke.  Meine Lösung ist der Pfeil in der unteren Grafik 2.

Zu deiner Frage:  Bei starren Verbindungen statt Seilen kann die Kraft am Verbindungspunkt in *alle* Richtungen wirken.

---

Deine Grafik ist leider sehr, sehr blaß und so
nicht zu lesen.

Wahrscheinlich müsste man bei Stabverbindungen
noch unterscheiden zwischen gelenkig,
starr, eingespannt usw.. Dies würde aber zu weit
führen.