Hebematte, Statik, 3D

Question

Aufgabe: Mat de levage

Die Abbildung zeigt ein technisches Diagramm, das ein System in einem dreidimensionalen Koordinatensystem darstellt.
• Das System besteht aus einer vertikalen Stange OA, die im Ursprung O befestigt ist.
• Ein Ausleger HD ist an der Stange befestigt, an dem eine Last ⃗ hängt.
• Zwei Seile, AB und AC, sichern die Stange und den Ausleger.
• Die Winkel und Längen sind angegeben: OA = h, HD = l, und verschiedene Winkel wie 60° und 45° definieren die Geometrie. Winkel „α“ unbekannt im Bild und Angaben.
• Das Diagramm wird typischerweise in der Statik verwendet, um Kräfte und Momente zu analysieren.

Ermitteln Sie die Spannkräfte in die Seilen (1 und 2) und die Reaktion des Bodens auf das Kugelgelenk beim Punkt O.

Problem/Ansatz:

Statik, 3D

Answer 1

die Aufgabe ist insgesamt etwas unklar, die Kräfte sollen in Abhängikeit welcher Parameter ermittelt werden? Stabil ist das System nur zwischen   \(-45°<\alpha<+45°\) . Ansonsten müssen die Kräfte in den Ebenen zerlegt und berechnet werden. Gibt es noch weitere Info?

Comments

Vielen Dank für Ihre Antwort,Überlegung und Frage.

Das ist das Problem für mich auch.

Da sind keine weitere Infos in der Aufgabe, leider!

Original Aufgabe:

Mat de levage
Le mat de levage suivant sert à soulever une charge de poids P. Il est articulé au point O et soutenu par deux haubans 1 et 2. Dans la position suivante, trouver la tension dans les haubans (1 et 2) et la réaction du sol sur la rotule en O.

Bitte um Hilfe obenzu.

Dankeschön

---

vereinfache das System in dem du vorerst die beiden Seile durch ein imaginäres Seil ersetzt (rot eingezeichnet). Dessen Seilkraft beträgt \(F_{Simg}=P\cdot\frac{l}{h}\).

Dann betrachtest du das System von oben und teilst F_Simg abhängig von α in die horizontalen Anteile der Seilkräfte auf. Letzlich lassen sich damit die Seilkräfte berechnen.

---

Hallo tomkelly,

wie sieht es denn aus? Kommst du weiter oder hakt es noch an manchen Stellen.

\(F_{s1}=\frac{1}{cos (60°)}\cdot cos(45°-\alpha)\cdot P\cdot\frac{l}{h}\)

über die Herleitung sollten wir uns aber noch austauschen!

---

Vielen Dank Karl60 für Ihre Antwort
Tolle 3D Darstellung (welche Software haben Sie hierzu benutz?), aber ich komme nicht weiter mit Ihrer Zeichnung.
Was ist F_s1 in Ihrer Zeichnung. Wie kommen Sie auf P = l/h, etc.
Wäre es möglich eine konkrete Lösung zu schreiben? Auch mit Skizze?
Dafür wäre ich sehr dankbar
Dankeschön im Voraus

---

die Darstellung habe ich mit Geogebra gemacht, hier in der 3D-Variante. F_S1 ist die Seilkraft im Seil 1, Wir machen weiter, wenn du den Schwerpunkt am Motorrad berechnet hast.

---

das schreibe ich hier um meinen Notizzettel wegwerfen zu können:

\(F_{s2}=\frac{1}{cos(60°)}\cdot sin(45°-\alpha)\cdot P\cdot \frac{l}{h}\)

wir können die Frage aber gerne weiter erörtern.

---

Danke Karl60

Und wie kommen Sie auf diese F_S2 - Formel?

Freundliche Grüsse

---

Sehr geehrte/r Karl60,
Danke für Ihre sparsame Antwort.
Ich finde es nicht in Ordnung, dass Sie mich ständig bei meinen Aufgaben – Fragen ohne Lösung dastehen lassen. D.h., dass Sie mich auf eine komische Art schikaniert haben.
Ich dachte hier in Nanolounge bekommt ein Schüler / Student Hilfe als Lösung, wenn er/ sie nicht weiterkommt, sodass er/ sie davon lernen kann.
Leider sind Sie komischerweise der / die einzige / n, der/ die mir bis jetzt überhaut geantwortet hat, und zwar nicht gerade richtig hilfreich. Wie Kommt das?
Ich bitte um Hilfe von der Nanolounge, sobald wie möglich, da ich eine grosse Prüfung über das Thema Statik in 2D und 3D am Montag, den 12.01.2026 habe.
Ich bedanke mich herzlichst im Voraus für die Mühe der Nanolounge. Bitte, helfen Sie mir, ich bin etwas verzweifelt; Ich brauche wirklich konkrete Lösungen, um von denen zu lernen…
Ganz freundliche Grüsse

---

Hallo tomkelly

es gibt andere Foren, in denen die Antworten noch deutlich "sparsamer" ausfallen. Was bringt es dir, wenn ich die Aufgabe vollständig vorrechne? Könntest du dann eine ähnliche Aufgabe lösen? Grundsätzlich kann es nur Hilfe zur Selbsthilfe geben.

Die Aufgabe ist folgendermaßen anzugehen:

in der Ebene 0HD muss das Hebelgesetz erfüllt sein, deswegen ist die horizontale Komponente der zusammengefassten Seilkräfte \(P\cdot \frac{l}{h}\) . Diese horizontale Komponente F_Simg teilt sich auf die Seile s1 und s2 auf. Von oben sieht das so aus:

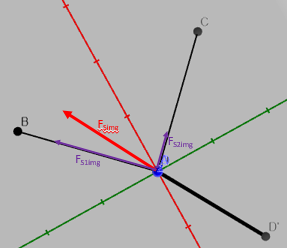
Und dann betrachten wir die einzelnen Seile von der Seite. Da kommt der Faktor \(\frac{1}{cos(60°)}\) hinzu.

Möge es dir helfen. Aber ohne Interaktion von eigenen Ansätzen mit Antworten aus diesem Forum ist das schwierig.

---

Bitte dringend um Hilfe bei der Aufgabe (!), von jedem Berater in der Nanolunge.

P.S.
Wenn ich die richtige Koordinate aller Punkte und aller Kräfte hätte, wüsste ich schon, wie der Lösungsweg ausschaut bzw. kann ich die Kräfte und Momente berechnen.

Vielen Dank im Voraus

Sehr freundliche Grüsse

---

Hallo,
Zitat von Karl60:
„Was bringt es dir, wenn ich die Aufgabe vollständig vorrechne? Könntest du dann eine ähnliche Aufgabe lösen?“
Antwort: Oh, ja, wenn Sie die Aufgabe hier nachvollziehbar lösen, dann kann ich mehrere ähnlichen Aufgaben alleine lösen.
Ihrer letzten Antwort nach ist die Lösung der Aufgabe absolut nicht begreiflich (!)
Und wieso, sind Sie Karl60, der /die einzige, der / die hier meine Fragen angeht und beantwortet?
Gibt’s keine anderen Berater in der Nanolounge?
Zitat von Karl60: «es gibt andere Foren, in denen die Antworten noch deutlich "sparsamer" ausfallen.“
Und welche anderen Foren sind diese?
Dankeschön
Freundliche Grüsse
P.S Bekomme ich die Lösung der Aufgabe oder nicht?

---

Oh, hallo nochmals.
Ah, Ah, Karl60, hier noch was, ich glaube Sie können gar keine Aufgabe in höheren technischer Mechanik 2D lösen, und in 3D sowieso nicht (!)
Sonst hätten Sie es getan, wenn / falls Sie es könnten, um Ihre Eitelkeit zu befriedigen (I).
Freundliche Grüsse

---

Hallo tomkelly,

bitte bedenke deine Wortwahl! Du fängst 10 Tage vor deiner Prüfung an hier Fragen zu stellen. Wenn es dann nicht hilft, ist nach deiner Meinung das Forum schuld.

Die Koordinaten sind A=( 0 | 0 | h ) ; H=( 0 | 0 | i ) ; D=( cos(α)·l | sin(α)·l | i ) ;

B=( -h·tan(30°)/√2 | -h·tan(30°)/√2 | 0 ) ;  C=( -h·tan(30°)/√2 | h·tan(30°)/√2 | 0 ).

Der Wert i spielt für die Seilspannung keine Rolle.