Wie ist die scheinbare Tiefe des Aquariums, wenn die Blickrichtung unter 35° zur Wasseroberfläche gerichtet ist?

Question

Hallo, hier eine Frage aus der Physik zum Thema Brechungsgesetz:

Wie ist die scheinbare Tiefe des Aquariums, wenn die Blickrichtung unter 35° zur Wasseroberfläche gerichtet ist? wahre Tiefe H = 1 m, n = 1,33

   

Danke

Answer 1

a = 35°;
H = 1m;
nL = 1;
nW = 1,33;

b = 90° -35° = 55°;

 

Brechungsgesetz:

nL*sin(b) = nW*sin(g);

g = arcsin( nL / nW * sin(b) );

 

Geometriebeziehungen:

d/H = tan(g); d = H * tan(g);

K/d = tan(a); K = d * tan(a);

 

Einsetzen:

K = H * tan{ arcsin( nL / nW * sin(b) )  } * tan(a);
K = 1m * tan{ arcsin( 1 / 1,33 * sin(55°) )  } * tan(35°) ≈ 0,5474m;

 

lg JR

 

Wie immer gilt: Kritisch prüfen. Bei Fragen, Fehlern, usw. --> Kommentar.

Answer 2

Hi,

in der Hoffnung keinen Denkfehler gemacht zu haben, bzw. falsch interpretiert zu haben ;).

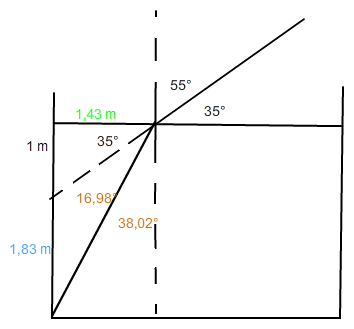
Sprich die 55° oben folgen aus 90°-35°.

Dann mit dem Snellius ran:

sin(55°)/sin(α)=1,33/1 --> α=38,02°

Daraus folgt auch direkt 16,98°.

 

Nun hat man ein rechtwinkliges Dreieck und die Höhe 1m bildet die Gegekathete zu den 35°. Die Ankathete lässt sich zu 1,43 m bestimmen (Hier hoffe ich, dass meine Interpretation von der Höhe korrekt ist).

 

Mit dem Bestimmen der Ankathete gehts nun an das Bestimmen der Höhe x:

x=tan(35°+16,98°)*1,43 m= 1,83 m

 

Grüße

Comments

Ui, da hatte ich wohl ne Weile nicht aktualisiert...

---

Also zwei Punkte möchte ich anmerken:

1. In der Aufgabenstellung steht, die wahre Wassertiefe betrage 1m. Das heißt die Strecke von der Wasseroberfläche bis zum Boden des Aquariums muss 1m betragen. Also kann es nicht das kurze Stück sein, das Du mit 1 m beschriftest (?).

2. Man kann ganz leicht ein Experiment machen und einen Stab in ein gefülltes Wasserglas halten. Wenn man den unter einem schrägen Winkel betrachtet, dann erscheint er verkürzt. Folglich sollte es sich bei der Aufgabe genauso verhalten, das heißt die scheinbare Tiefe muss geringer sein als die tatsächliche (Plausibilität des Ergebnisses). Selbst wenn die Brechungsindizes nicht übereinstimmen sollten, ist zumindest die Tendenz die gleiche, da es sich beim Wasser sowohl in der Aufgabenstellung (n=1,33) als auch beim Wasser im Experiment um ein optisch dichteres Medium handelt als bei Luft (Brechung zum Lot hin).

Vielleicht stehe ich auch komplett auf dem Schlauch. Aber da sich unsere Ergebnisse offensichtlich widersprechen, würde ich das schon gerne diskutieren. Ich denke das ist im Sinne des Fragenstellers und auch anderer Leute, die vielleicht über die Frage stolpern und nun nicht wissen welche Vorgehensweise richtig ist und vorallem warum.

---

Ja, ich da bin ich auch ein wenig gestolpert, wie ich die Aufgabe nun interpretieren darf. Letztlich hatte ich mich für meine Interpretation entschieden.

Ich hatte gewisse Probleme die "wahre" Tiefe zu identifizieren, da ich doch die dunkle Linie sehe, was ich auch als wahre Tiefe identifizieren würde. Somit konnte es nur die gestrichelte sein.

 

Eine Nacht darüber geschlafen, ist es aber ziemlich eindeutig Deine Interpretation ;).