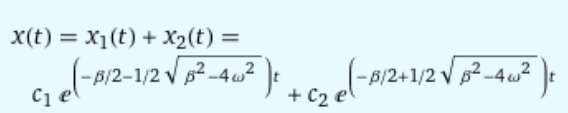Hallo,
Bestimmen Sie mit Hilfe eines Exponentialansatzes die allgemeine reelle Lösung der Bewegungsgleichung des gedämpften harmonischen Oszillators
Ansatz: x(t)= e^(k *t) , 2 Mal ableiten und in die DGL einsetzen:
->Charakteristische Gleichung:
k^2 +β k +ω^2=0
k1,2= -β/2 ± √((β^2/4) -ω^2)
k1,2= -β/2 ± √(β^2-4ω^2)/2
allgemeine Lösung: