Aufgabe:
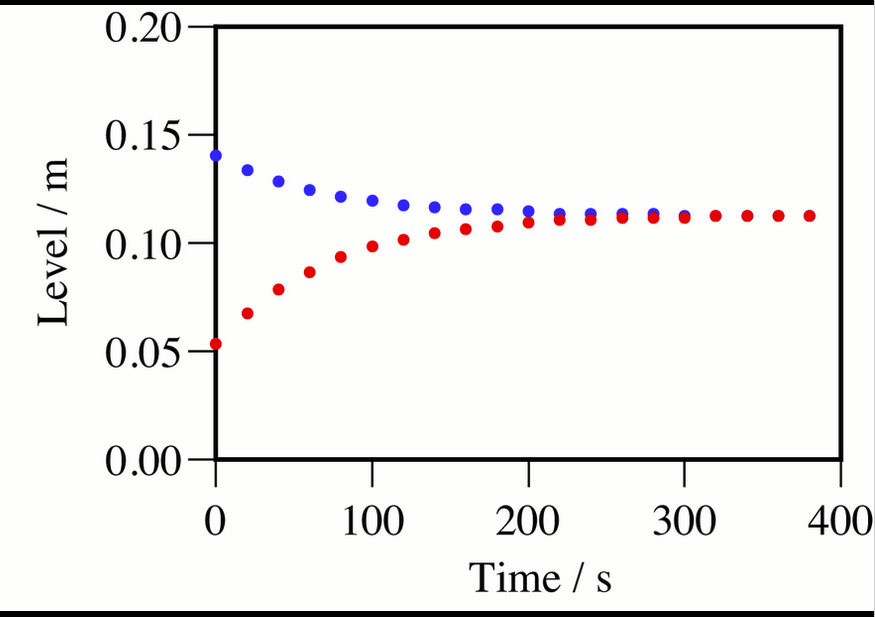
Wenn ich zwei Gefässe habe, die verbunden sind und sich wie im Diagramm verhalten. Die Radien der beiden Gefässe betragen 12 cm und 8.0 cm. Wie berechne ich den Leitwert und den Volumenstrom?
Problem/Ansatz:
Der Volumenstrom entspricht ja der Änderungsrate vom Vpunkt. Also kann ich ja einfach eine Tangente zeichnen und hätte: delta level / delta time = 0.1m / 100s => 0.001 m/s
Mit der Änderungsrate der Höhe kann ich V berechnen: 0.001 m/s * r1^2 * pi = 0.001 m/s * 0.12 * pi = 0.045 * 10^-3 m^3/s
Lösungen wäre aber: 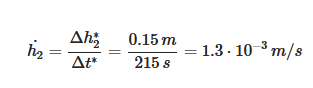
Text erkannt:
\( \dot{h_{2}}=\frac{\Delta h_{2}^{*}}{\Delta t^{*}}=\frac{0.15 m}{215 s}=1.3 \cdot 10^{-3} \mathrm{m} / \mathrm{s} \)
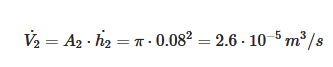
Text erkannt:
\( \dot{V}_{2}=A_{2} \cdot \dot{h_{2}}=\pi \cdot 0.08^{2}=2.6 \cdot 10^{-5} \mathrm{m}^{3} / \mathrm{s} \)
Wie kommt man auf diese Lösung?