Hallo,
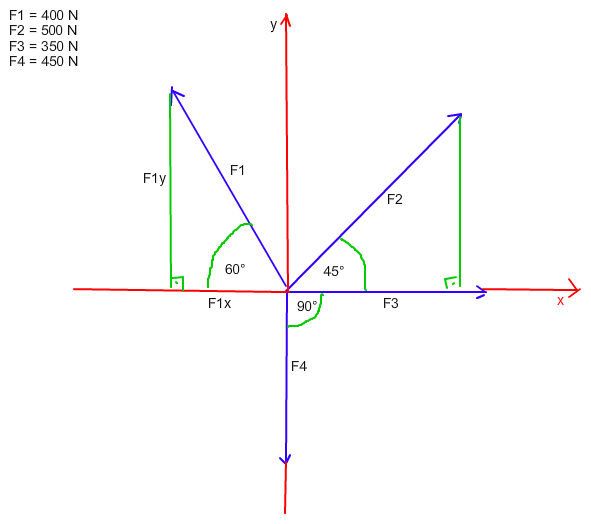
Jede der Kräfte hat eine x- und eine y- Komponente, die man ggf. mit den rechtwinkligen Dreiecken ausrechnen kann.
Wenn du jeweils die entsprechenden 4 Komponenten der Einzelkräfte addierst (bei F1x und F4y Minuszeichen beachten!) erhältst du die x-Komponente xR und die y-Komponente yR für die resultierenden Kraft. Deren Kraftpfeil hat dann den Endpunkt R(xR | yR)
Der Betrag r der resultierenden Kraft ist r = √(xR2 + yR2).
Je nachdem, in welchem Quadranten der Punkt (xR | yR) liegt erhält man den Winkel a der Resultierenden mit der positiven x-Achse aus a = ± arccos( xR / r ) . Das Minuszeichen steht bei negativem yR .
Sollte sich a negativ ergeben ( R im 3. oder 4. Quadranten), dann erhältst du den entsprechenden positiven Winkel, indem du zu a 360° addierst.
Gruß Wolfgang