Wenn ich es richtig entziffert habe (Browser-Einstellung 400 %) handelt es sich um ein t-v-Diagramm. Nach rechts wird die Zeit t in Sekunden und nach oben die Geschwindigkeit v in m/s abgetragen.
Die Bewegungsabläufe sind daher wie folgt abzulesen (Ich bezeichne die einzelnen Abschnitte (Zeitintervalle) von links nach rechts mit A, B, C bzw. D):
Im Zeitintervall A (t = 0 bis t = 5 s) hat der Wagen die Geschwindigkeit 0 m/s, steht also still.
Im Zeitintervall B (t = 5 bis t = 8 s) beschleunigt der Wagen gleichmäßig (konstante Steigung!) bis er eine Geschwindigkeit von 6 m / s erreicht hat.
Im Zeitintervall C (t = 8 bis t = 15 s) fährt der Wagen mit einer konstanten Geschwindigkeit von 6 m/s.
Im Zeitintervall D (t = 15 bis t = 16 s) bremst der Wagen gleichmäßig (konstante Steigung!) bis er eine Geschwindigkeit von 0 m / s erreicht hat.
Die von dem Wagen in der Zeit t = 0 bis t = 16 zurückgelegte Strecke entspricht dem Inhalt der Flächen, die der Graph in diesem Intervall mit der t-Achse einschließt. Bei dieser Fläche handelt es sich um ein Trapez mit der Grundseite a, der dieser Seite gegenüber liegenden Seite c und der Höhe h. Der Flächeninhalt A eines Trapezes mit diesen Bezeichnungen ist:
A = ( ( a + c ) / 2 ) * h
Es lässt sich ablesen:
a = 16 - 5 = 11 s
c = 15 - 8 = 7 s
h = 6 m/s
Einsetzen in die Formel ergibt für die Fläche A und damit auch für den zurückgelegten Weg s:
s = A = ( ( 11 + 7 ) / 2 * 6 = 54 m
Der Wagen legt also in den 16 Sekunden 54 Meter zurück (wobei er in den ersten 5 Sekunden in Ruhe ist).
b) Abschnitt A ( t = 0 bis t = 5 ) : Beschleunigung 0 m/s
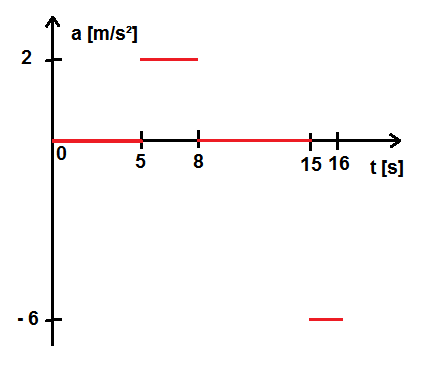
Abschnitt B (t = 5 bis t = 8) : Beschleunigung a = Δ v / Δ t = ( 6 m/s ) / ( 3 s ) = 2 m/s²
Abschnitt C: ( t = 8 bis t = 15 ) : Beschleunigung 0 m/s
Abschnitt D (t = 15 bis t = 16) : Beschleunigung a = Δ v / Δ t = ( - 6 m/s ) / ( 1 s ) = - 6 m/s²
Hier das t-a-Diagramm:
c) Die ab dem Zeitpunkt t = 0 zurückgelegte Strecke beträgt nach
5 s : 0 m
8 s : 0 m + ( 1 / 2 ) * 2 [m/s²] * ( ( 8 - 5 ) [s] ) ² = 9 m
15 s : 9 m + 6 [m/s] * 7 [s] = 51 m
16 s : 51 m + ( 1 / 2 ) * 6 [m/s²] * ( ( 16 - 15 ) [s] ) ² = 54 m
Das stimmt mit dem Ergebnis aus a) überein.
Hier das skizzierte t-s-Diagramm:
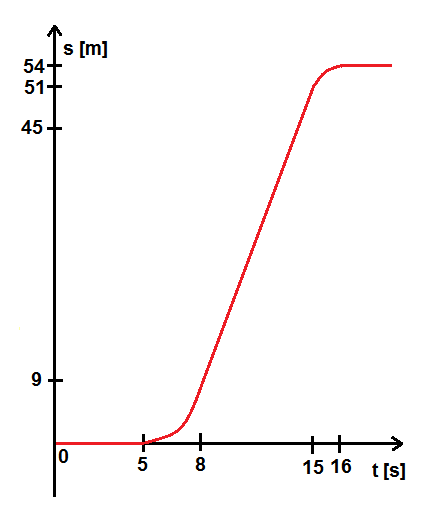
Erst ab t = 5 s beginnt der Wagen, einen Weg zurückzulegen. Da er bis t = 8 s beschleunigt, nimmt der zurückgelegte Weg mit dem Quadrat der Zeit zu, daher ist der Graph in diesem Abschnitt parabelförmig.
Ab t = 8 s fährt der Wagen mit einer konstanten Geschwindigkeit. Daher nimmt der zurückgelegte Weg linear zu - der Graph in diesem Abschnitt ist daher eine Gerade.
Ab t = 15 s bremst der Wagen. Die Zunahme des zurückgelegten Weges verlangsamt sich daher mit dem Quadrat der Zeit. Der Graph in diesem Abschnitt ist daher wieder parabelförmig, diese ist nun allerdings nach unten geöffnet. Ab t = 16 s nimmt der zurückgelegte Weg nicht mehr zu, da der Wagen zum Stillstand gekommen ist.