Hallo,
die Impulserhaltung bring Dir die Lösung. Und sie gilt (natürlich) auch im mehrdimensionalen. Allgemein gilt demnach $$\sum m_i\vec{v_i} = \text{konstant}$$
In einem Koordinatensystem in dem die erste Koordinatenrichtung nach Osten und die zweite nach Norden zeigt sind die beiden Geschwindigkeiten $$v_1 = 2\begin{pmatrix} \cos (-60°) \\ \sin(-60°) \end{pmatrix} \text{m/s} = 2\begin{pmatrix} \frac12 \\ -\frac12 \sqrt{3} \end{pmatrix} \text{m/s} \\ v_2 = 2 \begin{pmatrix} \cos (60°)\\ \sin(60°) \end{pmatrix} \text{m/s} = 2 \begin{pmatrix} \frac12 \\ \frac12 \sqrt{3} \end{pmatrix} \text{m/s}$$
Die Information "Nach dem Stoß haften die Körper aneinander." bedeutet, dass es nur noch eine resultierende Geschwindigkeit \(v_r\) für beide Massen gibt. Folglich ist $$m_1 \cdot v_1 + m_2 \cdot v_2 = (m_1+m_2) \cdot v_r$$
bzw. da die Massen beider Körper gleich sind $$m \cdot (v_1 + v_2) \\ \space = m \cdot \left( 2\begin{pmatrix} \frac12 \\ -\frac12 \sqrt{3} \end{pmatrix} \text{m/s} + 2 \begin{pmatrix} \frac12 \\ \frac12 \sqrt{3} \end{pmatrix} \text{m/s}\right) \\ \space = 2m \begin{pmatrix} 1 \\ 0 \end{pmatrix} \text{m/s} \\ \space = 2m v_r \quad \Rightarrow v_r = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \text{m/s}$$ nochmal als Skizze:
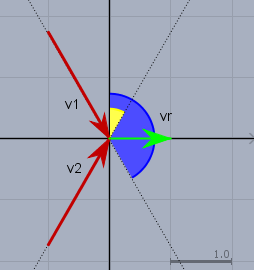
Gruß Werner