Magnetische Feldstärke: Für Punkt P drei magnetische Feldstärken, die von Gleichströmen herrühren, angeben

Question

Gebe für den Punkt P die Beiträge der 3 magnetischen Feldstärken, die von Gleichströmen I1, I2 und I3 herrühren an.

Zeichne dabei in die Darstellung die 3 Vektoren der magnetischen Feldstärke für den P in geeigneten Maßstab ein.

Die Gesamtfeldstärke soll dabei Null sein.

Ansatz : I1=I2=I; I3= k*I (k = konstante)

Könnt ihr mir bitte bei dieser Aufgabe helfen ?

Answer 1

Hallo

zeichne die 3 Kreise um I1, I2, I3 durch P die Feldstärke ist tangential an die Kreise und für I1 und I2 im Uhrzeigersinn auf dem Kreis, für Ir gegen den Uhrzeigersinn, B von I1 und I2 ist μ0*I/2*π*rPI) mit r=a*√2 für I1 und I2, a für I3  da sie senkrecht aufeinander stehen hann man sie nach Pythagoras addieren das Ergebnis zeigt  waagerecht nach links,  B von I3 nach rechts. wenn  du richtig rechnest muss I3=I1=I2 sein.

Gruß lul

Answer 2

Hallo,

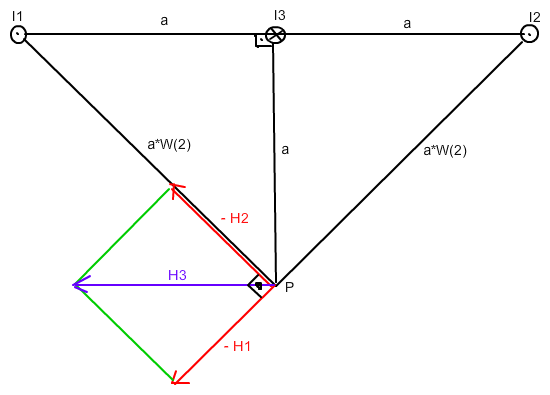
der Einfachheit halber benutze ich I1 , I2 und I3 auch als Namen für die Punkte in der Zeichnung:

Ich gehe von gleichen Stromstärken I₁ = I₂ = I  und I₃ = k·I aus.

Für den Betrag H der  magnetischen Feldstärke des Feldes eines stromdurchflossenen Drahtes in einem Punkt P mit Abstand r vom Draht gilt  H = I / (2π·r) 

→  H₁ = H₂  =  I / (2·√2·π·a)  ,  H₃  = I₃ / (2π·a)     (Beträge der Feldstärkevektoren)

Die Richtung von H ergibt sich jeweils tangential zu einem Kreis um den jeweiligen "Strompunkt" durch P (also senkrecht zur jeweiligen Verbindungslinie PI_k )

Aus der "Rechte-Hand-Regel" ergeben sich die eingezeichneten Richtungen bzw. (mit -) die Gegenrichtungen.

Der Betrag der Vektorsumme von - H₁ und - H₂  ist nach Pythagoras

√( 2·[I / (2·√2·π·a)]² )  =  I / (2π·a)

Wenn die Magnetfelder sich im Punkt P aufheben sollen, muss der Betrag dieser Vektorsumme gleich dem Betrag von  Vektor H₃  sein.

I₃  muss also dann genauso groß  wie I₁  bzw. I₂  sein.

Gruß Wolfgang

Comments

Wollte fragen, wie man anhand der Zeichnung herausfindet wie groß k zu wählen  ist.

Sry, dass ich erst jetzt diese Frage stelle.

---

\(|\vec{H_3}|=|\vec{H_1}+\vec{H_2}|\) 

weil die magnetischen Feldstärken sich dort aufheben sollen ("Die Gesamtfeldstärke soll dabei Null sein.")

Die Vektorpfeile von \(\vec{-H_1}\) und \(\vec{-H_2}\) bilden ein Quadrat mit der Diagonalenlänge  \(|\vec{H_3}|\)

→_Pythagoras   \(|\vec{H_3}|=\sqrt{|\vec{H_1}|^2+|\vec{H_2}|^2}\text{ }=\frac{I}{2π·a}\)

Außerdem gilt  \(|\vec{H_3}| =  \frac{I_3}{2π·a}\)

→  I = I₃   also k = 1

---

Und hättest du die Aufgabe auch lösen könne, wenn als erstes vor der Zeichnung-Aufgabe du die Rechnung zu den Beträgen der magnetischen Feldstärken anfertigen müsstest?

---

Die Zeichnung verdeutlicht eigentlich nur das, was im Text erläutert ist.