Du meinst vt-Diagramm in at-Diagramm umwandeln.
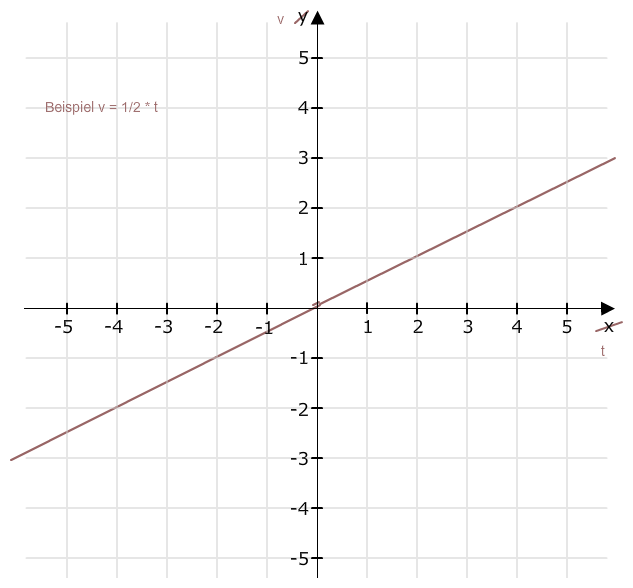
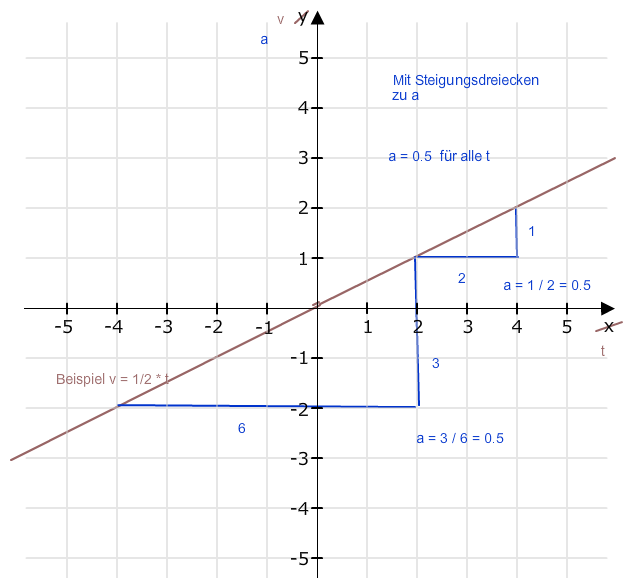
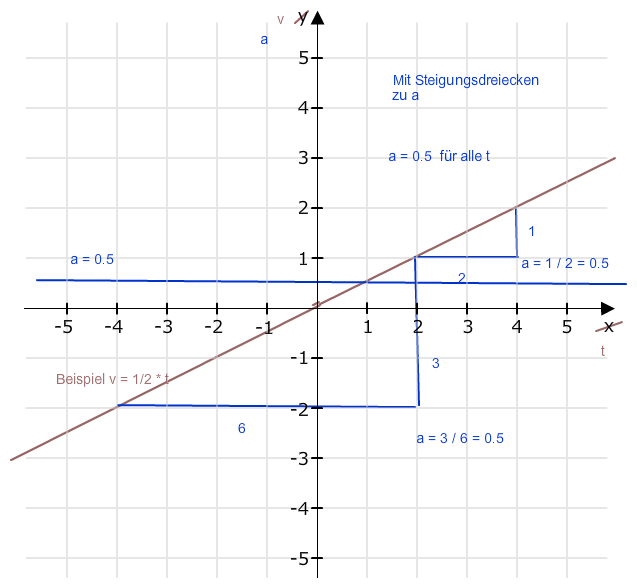
Jetzt zum st-Diagramm:
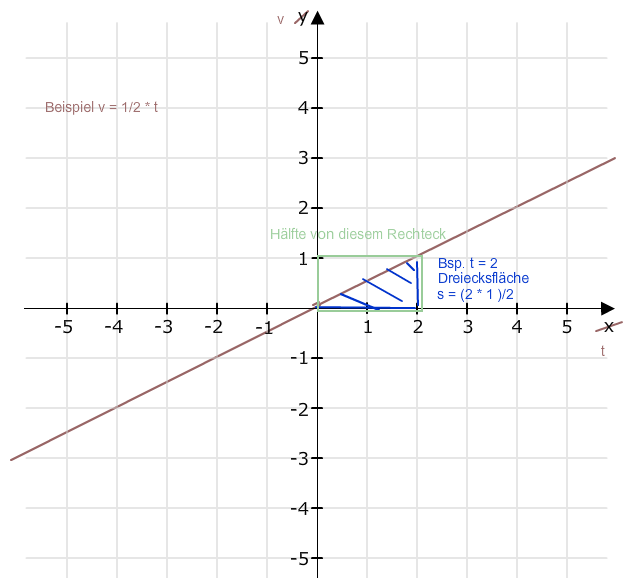
Bei t = 2 ist s = 1 . ==> Du hast einen Punkt auf dem Graphen im st-Diagramm.
Bei t = 3 ist s = 1/2 * 3 * 1.5 = 1.5^2 = 2.25 ==> Zweiter Punkt im st-Diagramm
usw.
Allgemein:
Bei t = t_o ist s = 1/2 * t_o * (a * t_o) = 1/2 a t_o^2
Skizze:
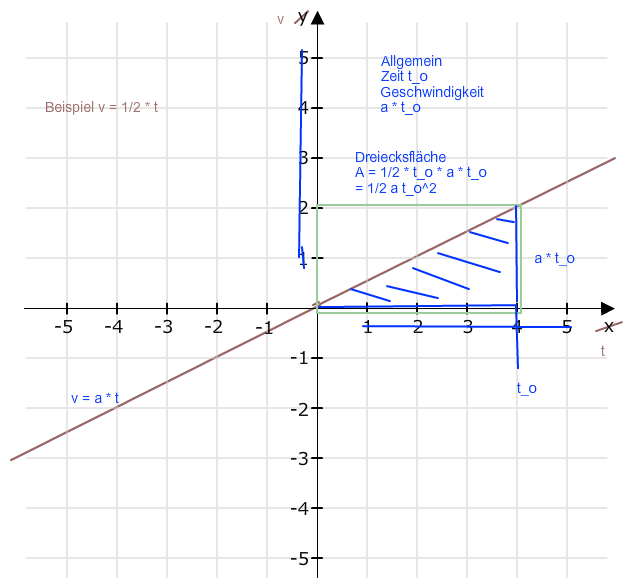
Nun war t_o ein beliebiges t. Daher gilt
s(t) = 1/2 a t^2