Teilströme in Abhängigkeit vom Widerstand und Spannung berechnen

Question

Fünf Widerstände R1, ..., R5 sind in Form einer Wheatstone-Brücke zusammengeschaltet. Man berechne die Teilströme I1, ..., I5 in Abhängigkeit von U und R, falls für die Widerstände gilt:
Rk: = k*R ( k∈{1, ..., 5}, U, R > 0 geeignet ) .

Answer 1

Hallo,

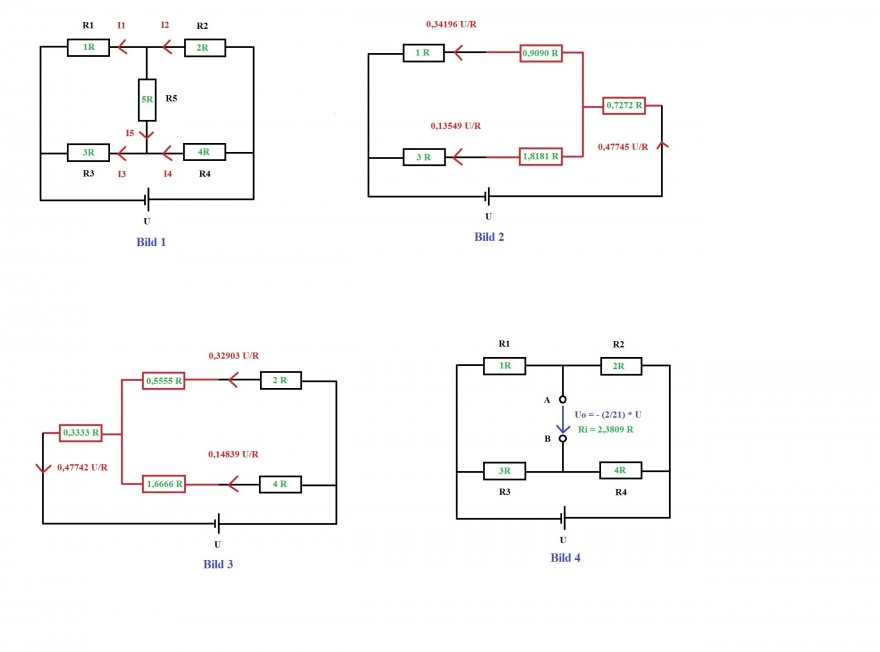
es sollen die Ströme  $$I_{1-5} = f(U;R_{1-5})$$ in allgemeiner Form berechnet werden, Bild 1.

Lösungsansatz:

I₁ und I₃ lassen sich berechnen, indem die Widerstände R₂ ; R₄ und R₅ in eine äquivalente Sternschaltung umgerechnet werden, Bild 2.

I₂ und I₄ lassen sich berechnen, indem die Widerstände R₁ ; R₃ und R₅ in eine äquivalente Sternschaltung umgerechnet werden, Bild 3.

I₅ lässt sich mit Hilfe einer Ersatzspannungsquelle zwischen den Klemmen A un B berechnen, Bild 4.

Berechnung der Ströme I₁ und I₃ :

Die Umrechnung der Widerstände in eine Sternschaltung ergibt Werte, wie in Bild 2 angegeben. Damit lässt sich der Gesamtwiderstand R_ges und der Gesamtstrom I_ges der Schaltung in allgemeiner Form berechnen:

$$R_{ges} =\text{  } 2,0945\text{  } R$$$$I_{ges} =\text{  } 0,47745\text{  } U/R$$Durch Anwendung der Stromteilerregel auf den Sternknoten erhält man die Ströme I₁ und I₃ :

$$I_{1} =\text{  } 0,34196\text{  } U/R$$$$I_{3} =\text{  } 0,13549\text{  } U/R$$

Berechnung der Ströme I₂ und I₄ :

Die Berechnung der Ströme I₂ und I₄ erfolgt auf die gleiche Weise, wobei jetzt die Widerstände R₁ , R₃ und R₅ in eine äquivalente Sternschaltung umgerechnet werden. Die entsprechenden Widerstandswerte zeigt Bild 3. Es leuchtet ein, dass der Gesamtwiderstand und der Gesamtstrom gegenüber der Berechnung von I₁ und I₃ gleich sein muss.

$$R_{ges} =\text{  } 2,0945\text{  } R$$$$I_{ges} =\text{  } 0,47745\text{  } U/R$$

Berechnung von I₅ :

Für die Ersatzspannungsquelle zwischen den Klemmen A und B erhält man folgende Werte, Bild 4:

$$U_{0} =\text{  }-\text{  }\frac{2}{21}*U$$$$R_{i} =\text{  } 2,3809\text{  } R$$

Damit kann I₅ berechnet werden

$$I_{5} =\text{  }-\text{  } 0,0129\text{  } U/R$$

Damit erhält man als Gesamtergebnis:

$$I_{1} =\text{  }\text{  } 0,34196\text{  } U/R$$$$I_{2} =\text{  }\text{  } 0,32903\text{  } U/R$$$$I_{3} =\text{  }\text{  } 0,13549\text{  } U/R$$$$I_{4} =\text{  }\text{  } 0,148387\text{  } U/R$$$$I_{5} =\text{  }-\text{  } 0,0129\text{  } U/R$$

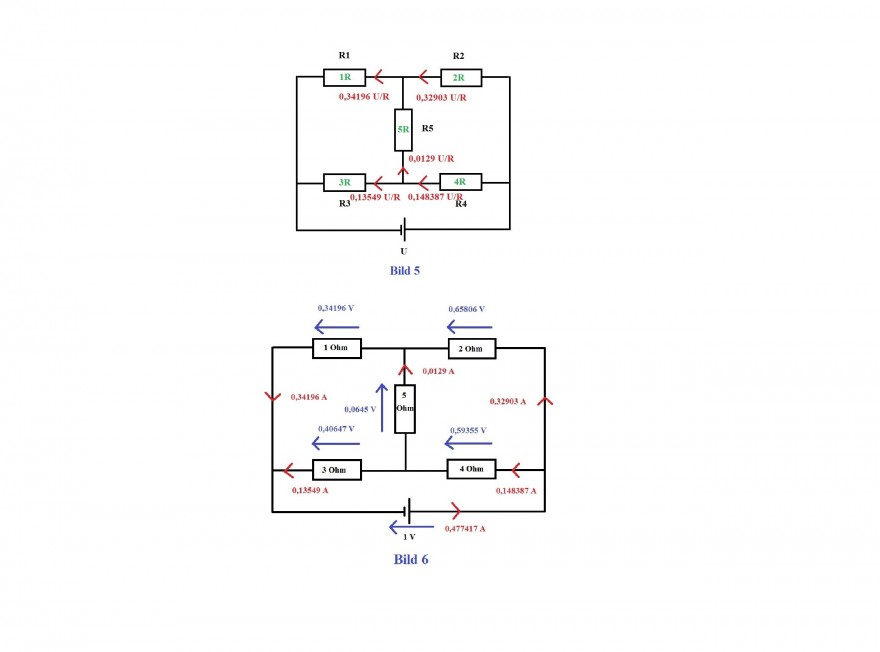
Alle Ströme zeigt Bild 5. Zur Kontrolle wurde ein Zahlenbeispiel mit folgenden Zahlenwerten berechnet:

U = 1 V

R = 1 Ω

Bild 6 zeigt die berechneten Werte.

Gruß von hightech