Hallo Hellin,
"... wie ich die Lagerreaktionen berechne?" Das läuft in identischer Weise wie hier.
Die Wirklinie der Kraft \(F_1\) geht durch das Lager \(A\) und hat damit keinen Einfluss auf die Kräfte im Punkt \(P\), der als Gelenk zwischen dem linken und rechten Teil des Fachwerks angesehen werden kann.
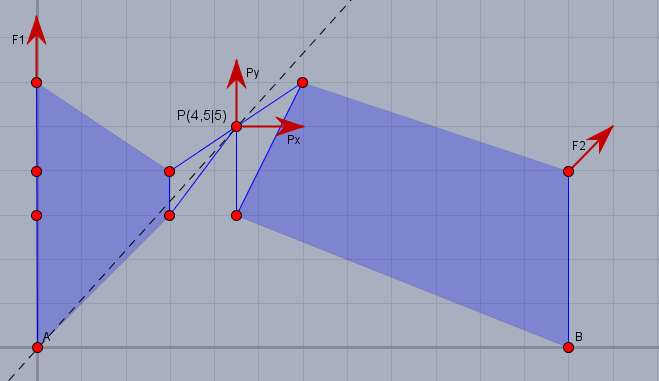
Damit liegt die Richtung der Kraft in \(P\) bereits fest. \(P_x\) und \(P_y\) seien die Kräfte, die im Punkt \(P\) auf den rechten Teil des Fachwerks wirken. Auf Grund der Geometrie muss gelten
$$\frac{P_x}{P_y} = \frac{4,5}{5}$$ Die Momentensumme um \(B\) gibt dann
$$-7,5a \cdot P_y - 5a \cdot P_x - 4a \cdot \frac12 \sqrt{2} F_2 = 0 $$ Einsetzen des Verhältnisses von oben gibt \(P_y\)
$$-7,5a \cdot P_y - 5a \cdot \frac{9}{10} P_y - 4a \cdot \frac12 \sqrt{2} F_2 = 0 \quad \Rightarrow P_y= \frac{-1}{6}\sqrt{2}F_2 $$ Und weiter ist dann \(P_x = \frac{-3}{20} \sqrt{2} F_2\). Die Lagerkräfte in \(A\) und \(B\) folgen jetzt aus den Kräftesummen in beiden Teilfachwerken. Für das rechte Fachwerk ist
$$P_x + B_x + \frac12 \sqrt{2} F_2 = 0 \quad \Rightarrow B_x = \frac{-7}{20} \sqrt{2} F_2$$ $$P_y + B_y + \frac12 \sqrt{2} F_2 = 0 \quad \Rightarrow B_y = \frac{-1}{3} \sqrt{2} F_2$$ und für das linke Fachwerk $$A_x - P_x = 0 \quad \Rightarrow A_x = \frac{-3}{20} \sqrt{2} F_2$$ $$F_1 + A_y - P_y = 0 \quad \Rightarrow A_y = \frac{-1}{6} \sqrt{2} F_2 - F_1$$ Gruß Werner