Hallo, hier die Lösung der Aufgabe:
Wenn der Schalter geschlossen ist, wird der Kondensator C1 über R2 aufgeladen. Auf den Ladevorgang hat der Widerstand R1 keinen Einfluss.
Die Zeitkonstante für den Ladevorgang errechnet sich zu: τL = C1 • R2 = 1µF • 1 KΩ = 1 ms
Wenn der Schalter geöffnet ist, wird der Kondensator über R1 und R2 entladen.
Die Zeitkonstante für den Entladevorgang errechnet sich zu: τE = C1 • (R1 + R2 ) = 1µF • 2 KΩ = 2 ms
Die Gleichung für den Ladevorgang lautet: UC = UC,t0 • e-t/τL + U0 • (1 - e-t/τL )
mit UC Kondensatorspannung
UC,t0 Kondensatorspannung zu Beginn des Ladevorgangs (ist Null zu Beginn des ersten Ladevorgangs)
U0 Spannung der Quelle
Die Gleichung für den Entladevorgang lautet: UC = UC,E • e-t/τE
mit UC Kondensatorspannung
UC,E Kondensatorspannung zu Beginn des Entladevorgangs
Mit diesen Gleichungen, den Zeitkonstanten und der Spannung der Quelle lassen sich die Ladespannungen und Entladespannungen (nach 5 ms, 10 ms, 15 ms, 20 ms) ausrechnen:
Hier die errechneten Werte:
nach 5 ms nach 10 ms nach 15 ms nach 20 ms
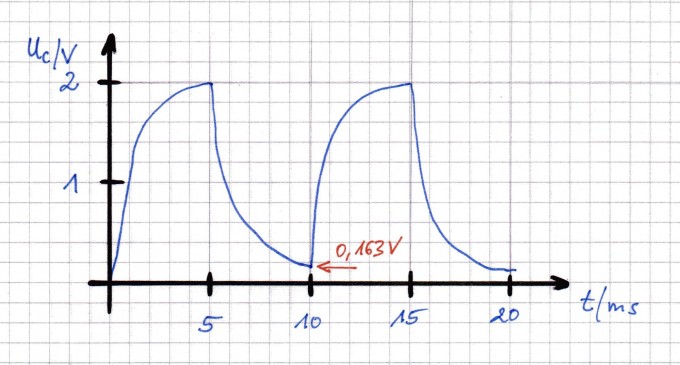
UC = 1,9865V 0,1631V 1,9876V 0,1631V , (dem Entladevorgang hat der Kondensator noch eine Spannung von 0,1631V). Die Spannungswerte sind in das Diagramm unten eingezeichnet.