Vektoren: Welchen Kompasskurs muss die Pilotin einstellen, damit sie genau in Richtung Norden fliegt?

Question

Aufgabe:

Ein Flugzeug fliegt mit einer Geschwindigkeit von 280 km/h relativ zur Luft. Ein Sturm weht genau aus Südost (Kompassrichtung 315  ◦) mit 90 km/h.

a) Welchen Kompasskurs muss die Pilotin einstellen, damit sie genau in Richtung Norden fliegt?

b) Welche Geschwindigkeit über Grund hat das Flugzeug auf diesem Nordkurs?

Answer 1

Hallo,

Dieses Problem nennt man Winddreieck (bzw. Strömungsdreieck in der Schifffahrt). Stelle Dir vor, man könnte in einer  Stunde Flug den Versatz durch den Sturm und den Flug getrennt betrachten. Angenommen, das Flugzeug bewegt sich nicht gegenüber Luft und wird nur vom Wind versetzt. Dann würde es sich nach einer Stunde 90km nordwestlich befinden. Jetzt halte den Sturm in Gedanken an und überlege, in welche Richtung die Pilotin fliegen müsste um sich nach 280km genau auf der Nordlinie zu befinden. Folgende Skizze zeigt das:

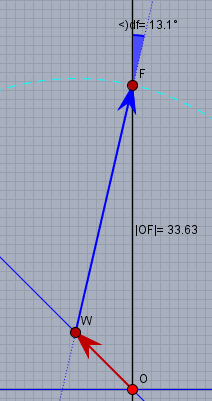  (M 1:10)

Betrachte das Dreieck \(OFW\), oben der blaue Winkel sei \(\varphi\) und ist der Kompasskurs, und wende den Sinussatz an:

$$\frac{\sin( \varphi )}{ 90 } = \frac{ \sin( 45° ) }{280} \quad \Rightarrow \varphi= \arcsin \left(90 \cdot \frac{ \sin( 45° ) }{280} \right) \approx 13,14°$$

Die Geschwindigkeit \(v_G\) über Grund kann man auch über den Sinussatz bestimmen

$$\frac{v_G}{\sin(180° - 45° - 13,14°)}=\frac{ 280\text{km/h}}{\sin(45°)} \quad \Rightarrow v_G\approx 336,3 \text{km/h}$$

Gruß Werner

Answer 2

a) & b)

90/√2·[-1, 1] + 360·[sin(α°), cos(α°)] = [0, y] --> y = 418.0 ∧ α = 10.18°