Hallo Holdi,
wir machen 'mal weiter. Das "Drehlager" das du beschreibst ist keins, ich mag mich undeutlich ausgedrückt haben. Es könnte auch so aussehen:
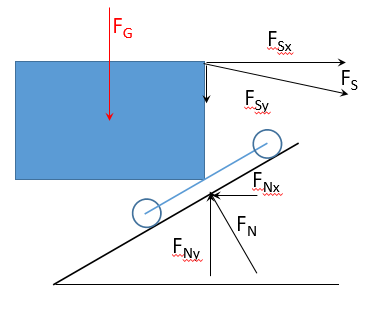
Meine Rechnung
1. \(\Sigma\) Momente: \(F_G \cdot 0,4 m=F_{Sx}\cdot 0,5 m\)
2. \(\Sigma\) \(F_x\): \(F_{Nx}=F_{Sx}\)
3. \(\Sigma\) \(F_y\): \(F_{Ny}=F_G+F_{Sy}\)
keine Kräfte am Berührungspunkt parallel zur schiefen Ebene, deswegen:
4. \(\frac{F_{Nx}}{F_{Ny}}=tan(30°)\) oder \(F_{Nx}=tan(30°)\cdot F_{Ny}\)
4. in 2. eingesetzt: \(F_{Sx}=tan(30°)\cdot F_{Ny}\)
das in 1. eingesetzt: \(F_G \cdot 0,4 m=tan(30°)\cdot F_{Ny}\cdot 0,5 m\)
\(F_{Ny}\) durch 3. ersetzt: \(F_G \cdot 0,4 m=tan(30°)\cdot (F_G+F_{Sy})\cdot 0,5 m\)
hier ist nur noch \(F_{Sy}\) unbekannt, nach \(F_{Sy}\) umgestellt ergibt \(F_{Sy}=3856N\) ; dann ist \(F_{Ny}=13856N\) und \(F_{Nx}=F_{Sx}=8000N\) ;
ergibt \(F_S=8881N\) und \(\beta=64,3°\) .
Auch hier ist wieder eine gewisse Wahrscheinlichkeit eines Rechenfehlers vorhanden, zur Zeit sehe ich aber nur diese eine Lösung. Ebenso ist mir klar, dass es Gleichungssyteme mit unendlich vielen Lösungen gibt, die Bedingungen dafür sehe ich hier aber nicht.
Ich freue mich auf Kommentare!
