Wie groß ist das Moment des Kräftepaars um die y-Achse?

Question

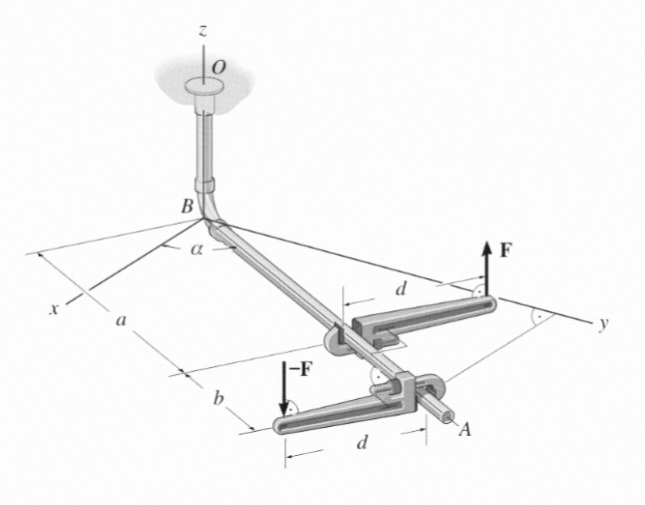
Das resultierende Moment des Kräftepaars, das am Rohr angreift, ist M.

a) Bestimmen Sie den erforderlichen Betrag F der an den Rohrzangen an- greifenden Kräfte. Wählen Sie hierfür ein geeignetes Koordinatensystem.

Gegeben: M = 15 Nm, a = 300 mm, b = 150 mm, d = 200 mm, α = 60°

b) Wie groß ist das Moment des Kräftepaars um die y-Achse? Verwenden Sie F 40 N.

Problem/Ansatz:

Aufgabe a) habe ich so gelöst

M=2Fd

F=M/2d

F=15/0,4

F=37,5

Answer 1

eine etwas unklare Aufgabe.

Das Drehmoment entlang des waagerechten Rohres ändert sich, gemeint ist wohl M = 15 N im Punkt B. Und somit hast du das für a) richtig berechnet. Das geeignete Koordinatensystem ist die Ebene ABO.

Zu b): das Moment M = 15 N ist ein Vektor in der xy-Ebene, diesen Vektor kannst du in x- und y-Anteil zerlegen.

M_y = M · sin (α) =15 Nm·sin (60°) ≈ 12,99 Nm. Die gegebene Kraft F=40 N sehe ich hier als ünerflüssig an.

Comments

die Rechnung für b) habe ich korrigiert.

---

Danke, wäre es vielleicht sinnvoll, eine Rotationsmatrix um die z-Achse zu legen? ( nur Überlegungen von mir) Und bei aufgabe b) soll man die Kraft F=40N verwenden.  

---

die Rotationsmatrix ist eine sehr gute Idee.

In Aufgabe b ergibt sich mit der Kraft F = 40 N ein Moment von 16 Nm. In y-Richtung ist der Anteil dann 13,86 Nm

---

\( R_{z}\left(60^{\circ}\right)=\left[\begin{array}{ccc}\cos 60^{\circ} & \sin 60^{\circ} & 0 \\ -\sin 60^{\circ} & \cos 60^{\circ} & 0 \\ 0 & 0 & 1\end{array}\right] \)

Wäre die Matrix so richtig?