Aufgabe:
Text erkannt:
Aufgabe 3
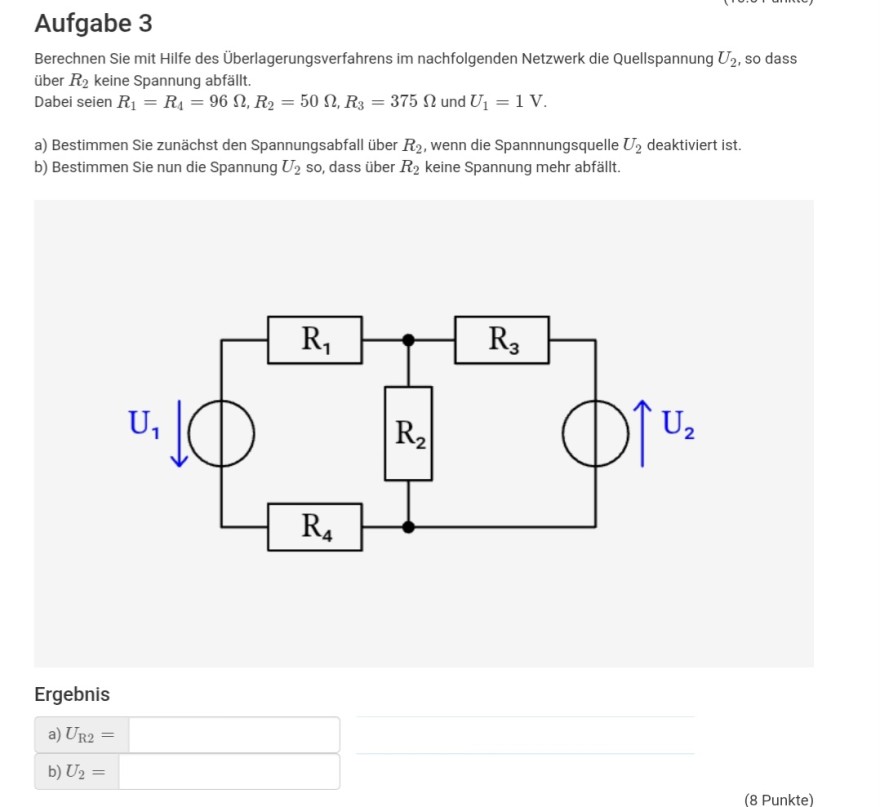
Berechnen Sie mit Hilfe des Überlagerungsverfahrens im nachfolgenden Netzwerk die Quellspannung \( U_{2} \), so dass über \( R_{2} \) keine Spannung abfällt.
Dabei seien \( R_{1}=R_{4}=96 \Omega, R_{2}=50 \Omega, R_{3}=375 \Omega \) und \( U_{1}=1 \mathrm{~V} \).
a) Bestimmen Sie zunächst den Spannungsabfall über \( R_{2} \), wenn die Spannnungsquelle \( U_{2} \) deaktiviert ist.
b) Bestimmen Sie nun die Spannung \( U_{2} \) so, dass über \( R_{2} \) keine Spannung mehr abfällt.
Ergebnis
a) \( U_{\mathrm{R} 2}= \)
b) \( U_{2}= \)
(8 Punkte)
Text erkannt:
(7 Punkte)
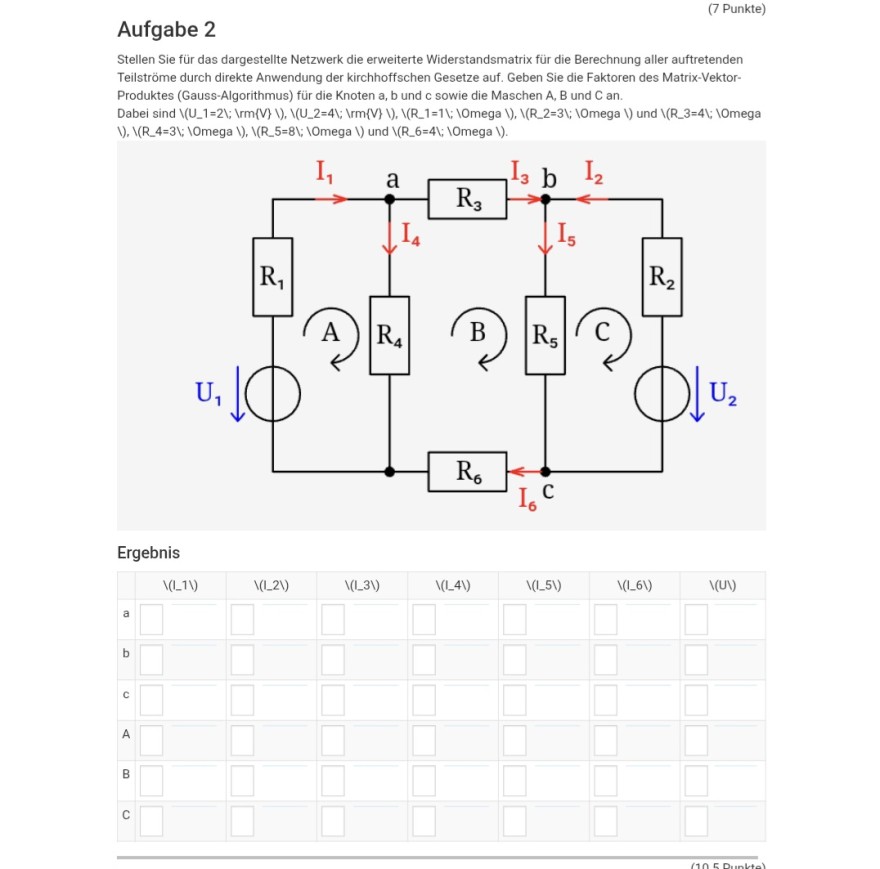
Aufgabe 2
Stellen Sie für das dargestellte Netzwerk die erweiterte Widerstandsmatrix für die Berechnung aller auftretenden Teilströme durch direkte Anwendung der kirchhoffschen Gesetze auf. Geben Sie die Faktoren des Matrix-VektorProduktes (Gauss-Algorithmus) für die Knoten \( \mathrm{a}, \mathrm{b} \) und c sowie die Maschen \( \mathrm{A}, \mathrm{B} \) und C an. ), \( \backslash( \) R_4 \( =3 \backslash \); \( \backslash 0 \) mega \( \backslash), \backslash( \) R_5=8 \( \backslash \); \( \backslash \) Omega \( \backslash \) ) und \( \backslash( \) R_6=4 \( \backslash \); \( \backslash \) Omega \( \backslash \) ).
Ergebnis
\begin{tabular}{|l|l|l|l|l|l|l|l|l|}
\hline & \\(L_1) & & \\(1_21) & \\(L_31) & \\(L_41) & \\(1_5) & \\(L_61) & \\(U) \\ \hline a & \( \square \) & \( \square \) & & \( \square \) & \( \square \) & \( \square \) & \( \square \) & \( \square \) \\
\hline b & \( \square \) & \( \square \) & & \( \square \) & \( \square \) & \( \square \) & \( \square \) & \( \square \) \\
\hline c & \( \square \) & \( \square \) & & \( \square \) & \( \square \) & \( \square \) & \( \square \) & \( \square \) \\
\hline A & \( \square \) & \( \square \) & & \( \square \) & \( \square \) & \( \square \) & \( \square \) & \( \square \) \\
\hline B & \( \square \) & \( \square \) & & \( \square \) & \( \square \) & \( \square \) & \( \square \) & \( \square \) \\
\hline C & \( \square \) & \( \square \) & & \( \square \) & \( \square \) & \( \square \) & \( \square \) & \( \square \) \\
\hline
\end{tabular}
Text erkannt:
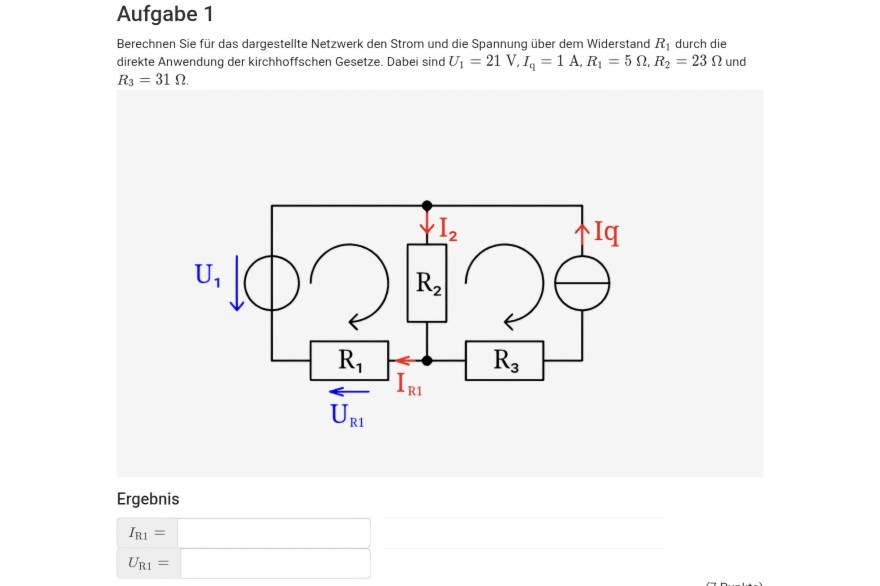
Aufgabe 1
Berechnen Sie für das dargestellte Netzwerk den Strom und die Spannung über dem Widerstand \( R_{1} \) durch die direkte Anwendung der kirchhoffschen Gesetze. Dabei sind \( U_{1}=21 \mathrm{~V}, I_{\mathrm{q}}=1 \mathrm{~A}, R_{1}=5 \Omega, R_{2}=23 \Omega \) und \( R_{3}=31 \Omega \).
Ergebnis
\( \begin{array}{l} I_{\mathrm{R} 1}= \\ U_{\mathrm{R} 1}=\square \end{array} \)
Text erkannt:
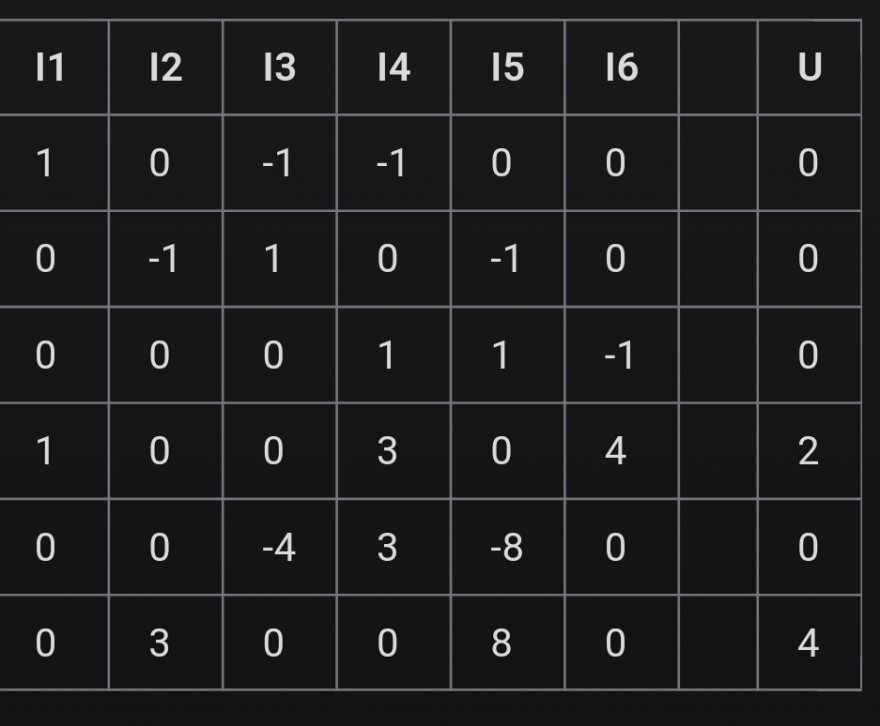
\begin{tabular}{|l|l|l|l|l|l|l|}
\hline I1 & 12 & I3 & 14 & 15 & I6 & U \\
\hline 1 & 0 & -1 & -1 & 0 & 0 & 0 \\
\hline 0 & -1 & 1 & 0 & -1 & 0 & 0 \\
\hline 0 & 0 & 0 & 1 & 1 & -1 & 0 \\
\hline 1 & 0 & 0 & 3 & 0 & 4 & 2 \\
\hline 0 & 0 & -4 & 3 & -8 & 0 & 0 \\
\hline 0 & 3 & 0 & 0 & 8 & 0 & 4 \\
\hline
\end{tabular}
Problem/Ansatz:
Ich verstehe die ganze Sache nicht ganz.
Sind meine Werte so richtig?
Aufgabe 1
I_R1 = 4,2 A
U_R1 = 21
Aufgabe 3
a) U_R2 ≈ 0,315 V
b) U2 = 0,5 V