Text erkannt:
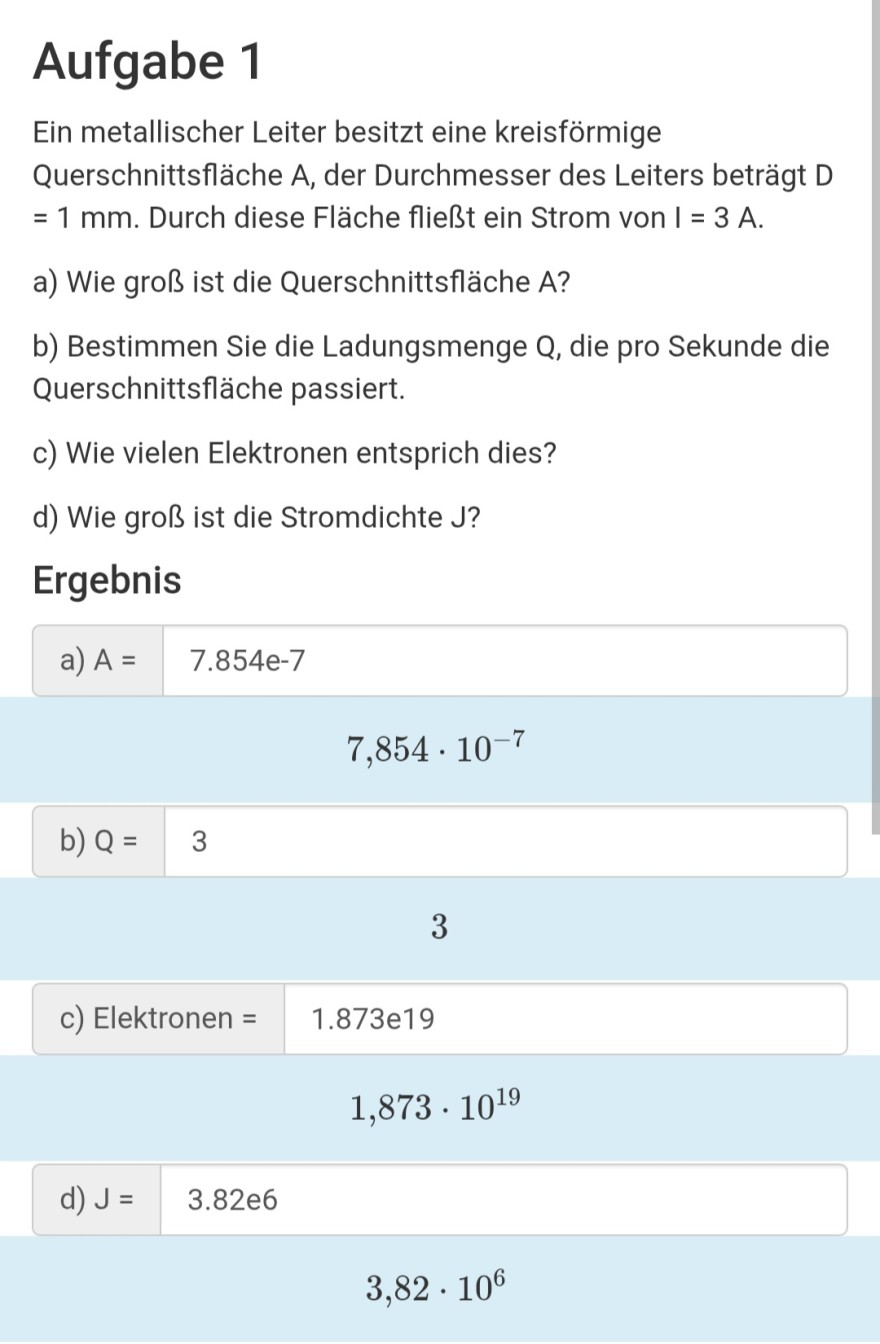
Aufgabe 1
Ein metallischer Leiter besitzt eine kreisförmige Querschnittsfläche A, der Durchmesser des Leiters beträgt D \( =1 \mathrm{~mm} \). Durch diese Fläche fließt ein Strom von I = 3 A .
a) Wie groß ist die Querschnittsfläche \( A \) ?
b) Bestimmen Sie die Ladungsmenge Q , die pro Sekunde die Querschnittsfläche passiert.
c) Wie vielen Elektronen entsprich dies?
d) Wie groß ist die Stromdichte J?
Ergebnis
a) \( A=7.854 e-7 \)
\( 7,854 \cdot 10^{-7} \)
b) \( Q=3 \)
3
c) Elektronen \( =1.873 \mathrm{e} 19 \)
\( 1,873 \cdot 10^{19} \)
d) \( J=3.82 e 6 \)
\( 3,82 \cdot 10^{6} \)
Text erkannt:
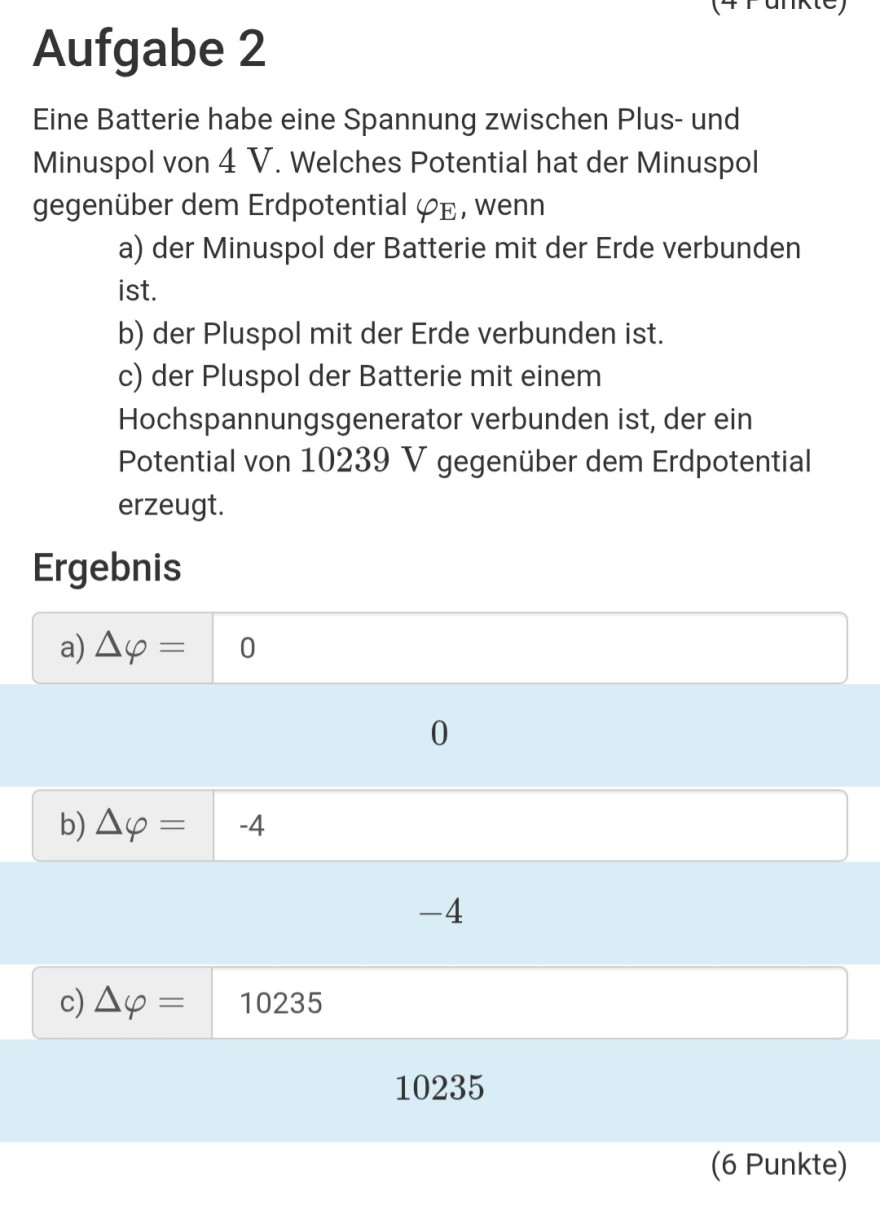
Aufgabe 2
Eine Batterie habe eine Spannung zwischen Plus- und Minuspol von 4 V . Welches Potential hat der Minuspol gegenüber dem Erdpotential \( \varphi_{\mathrm{E}} \), wenn
a) der Minuspol der Batterie mit der Erde verbunden ist.
b) der Pluspol mit der Erde verbunden ist.
c) der Pluspol der Batterie mit einem Hochspannungsgenerator verbunden ist, der ein Potential von 10239 V gegenüber dem Erdpotential erzeugt.
Ergebnis
а) \( \Delta \varphi=\quad 0 \)
0
b) \( \Delta \varphi=-4 \)
-4
c) \( \Delta \varphi=10235 \)
10235
(6 Punkte)

Text erkannt:
Aufgabe 3
Das ohm'sche Gesetz stellt einen Zusammenhang von Strom \( I \), Spannung \( U \) und dem Widerstand \( R \) her. Dabei gilt \( U=R \cdot I \). Leiten Sie daraus die Einheit
a) des Widerstandes
b) und des spezifisches Widerstands
im mksA-System ab.
Ergebnis
a)
\( \Omega=\left[\begin{array}{c}\left(\mathrm{kg}^{*} \mathrm{~m}^{\wedge} 2\right) /\left(\mathrm{s}^{\wedge} 3^{*} \mathrm{~A}^{\wedge} 2\right) \\ \frac{k \mathrm{~g} \cdot \mathrm{~m}^{2}}{\mathrm{~s}^{3} \cdot \mathrm{~A}^{2}}\end{array}\right] \)
Sie haben keine gültige Einheit angegeben!
\begin{tabular}{|c|c|}
\hline b) \( \varrho= \) & \( \left(\mathrm{kg}^{*} \mathrm{~m}^{\wedge} 3\right) /\left(\mathrm{s}^{\wedge} 3 * \mathrm{~A}^{\wedge} 2\right) \) \\
\( \frac{\mathrm{kg} \cdot \mathrm{m}^{3}}{\mathrm{~s}^{3} \cdot \mathrm{~A}^{2}} \) & \( \times \) T
\end{tabular}
Leere Eingabe!
Text erkannt:
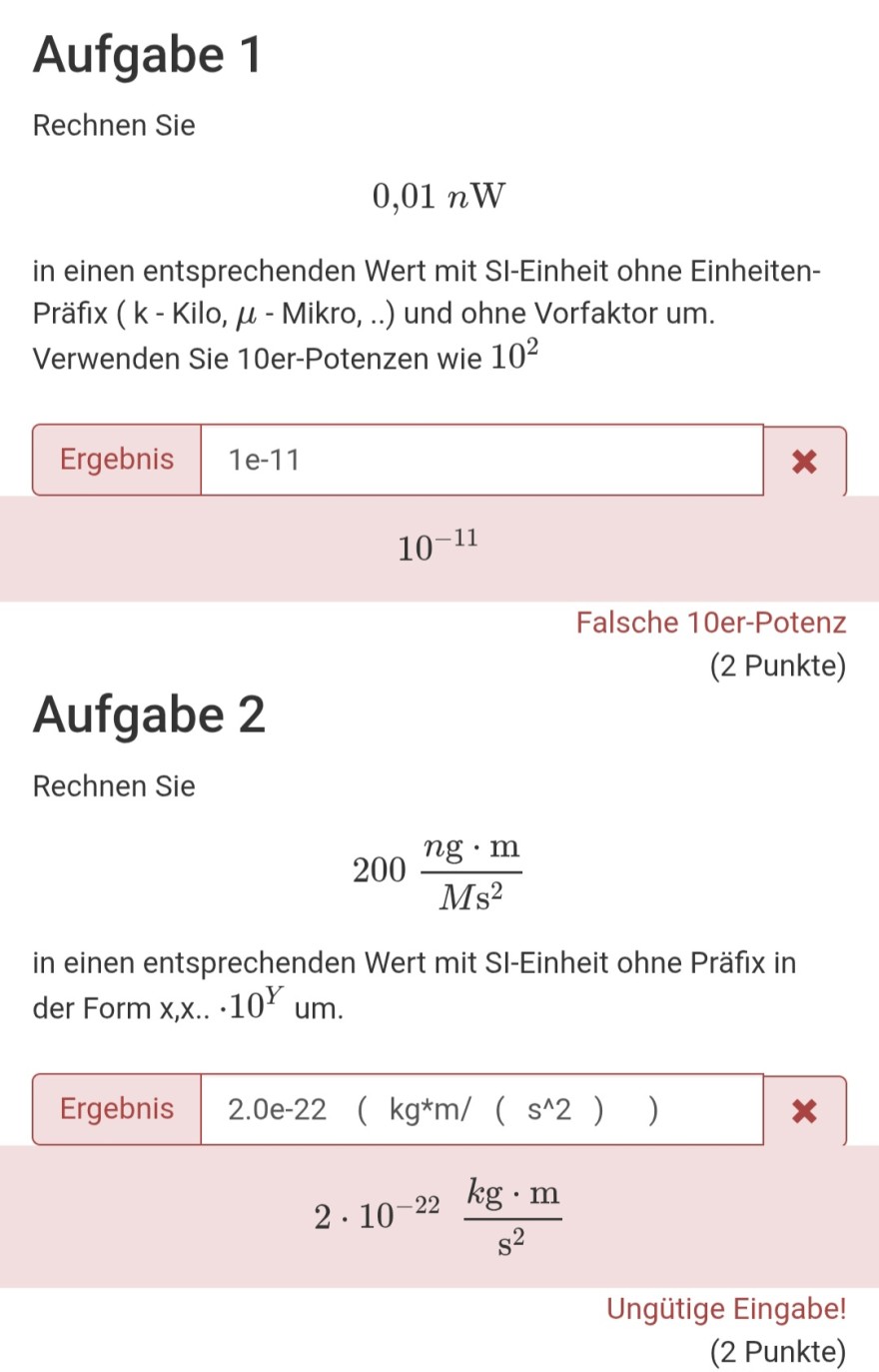
Aufgabe 1
Rechnen Sie
\( 0,01 n \mathrm{~W} \)
in einen entsprechenden Wert mit SI-Einheit ohne EinheitenPräfix ( k - Kilo, \( \mu \) - Mikro, ..) und ohne Vorfaktor um. Verwenden Sie 10er-Potenzen wie \( 10^{2} \)
\begin{tabular}{|l|l|}
\hline Ergebnis & \( 1 \mathrm{e}-11 \) \\
\hline
\end{tabular}
\( 10^{-11} \)
Falsche 10er-Potenz
(2 Punkte)
Aufgabe 2
Rechnen Sie
\( 200 \frac{n \mathrm{~g} \cdot \mathrm{~m}}{M \mathrm{~s}^{2}} \)
in einen entsprechenden Wert mit SI-Einheit ohne Präfix in der Form \( \mathrm{x}, \mathrm{x} . . \cdot 10^{Y} \) um.
\begin{tabular}{|c|}
\hline Ergebnis \\
\( 2.0 \mathrm{e}-22\left(\mathrm{~kg} * \mathrm{~m} /\left(\mathrm{s}^{\wedge} 2\right)\right) \) \\
\( 2 \cdot 10^{-22} \frac{\mathrm{~kg} \cdot \mathrm{~m}}{\mathrm{~s}^{2}} \)
\end{tabular}
Ungütige Eingabe!
(2 Punkte)
Text erkannt:
Aufgabenblatt
\( ? \)
Ergebnis \( 2.0 \mathrm{e}-22 \mathrm{~kg} * \mathrm{~m} / \mathrm{s}^{\wedge} 2 \)
\( 2 \cdot 10^{-22} \frac{\mathrm{~kg} \cdot \mathrm{~m}}{\mathrm{~s}^{2}} \)
(2 Punkte)
Aufgabe 3
Das ohm'sche Gesetz stellt einen Zusammenhang von Strom \( I \), Spannung \( U \) und dem Widerstand \( R \) her. Dabei gilt \( U=R \cdot I \). Leiten Sie daraus die Einheit
a) des Widerstandes
b) und des spezifisches Widerstands
im mksA-System ab.
Ergebnis
a) \( \Omega=\mathrm{kg} \mathrm{m}^{\wedge} 2 / \mathrm{A}^{\wedge} 2 \mathrm{~s}^{\wedge} 3 \)
\( \frac{\mathrm{kg} \cdot \mathrm{~m}^{2}}{\mathrm{~A}^{2} \cdot \mathrm{~s}^{3}} \)
Sie haben keine gültige Einheit angegeben!
b) \( \varrho=\mathrm{kg} \mathrm{m}^{\wedge} 3 / \mathrm{A}^{\wedge} 2 \mathrm{~s}^{\wedge} 3 \)
\( \frac{\mathrm{kg} \cdot \mathrm{~m}^{3}}{\mathrm{~A}^{2} \cdot \mathrm{~s}^{3}} \)
Aufgabe:
Problem/Ansatz:
… Was ist hier die Problem? Es sollte alles richtig sein, trotzdem sieht das Rot falsch angezeigt.