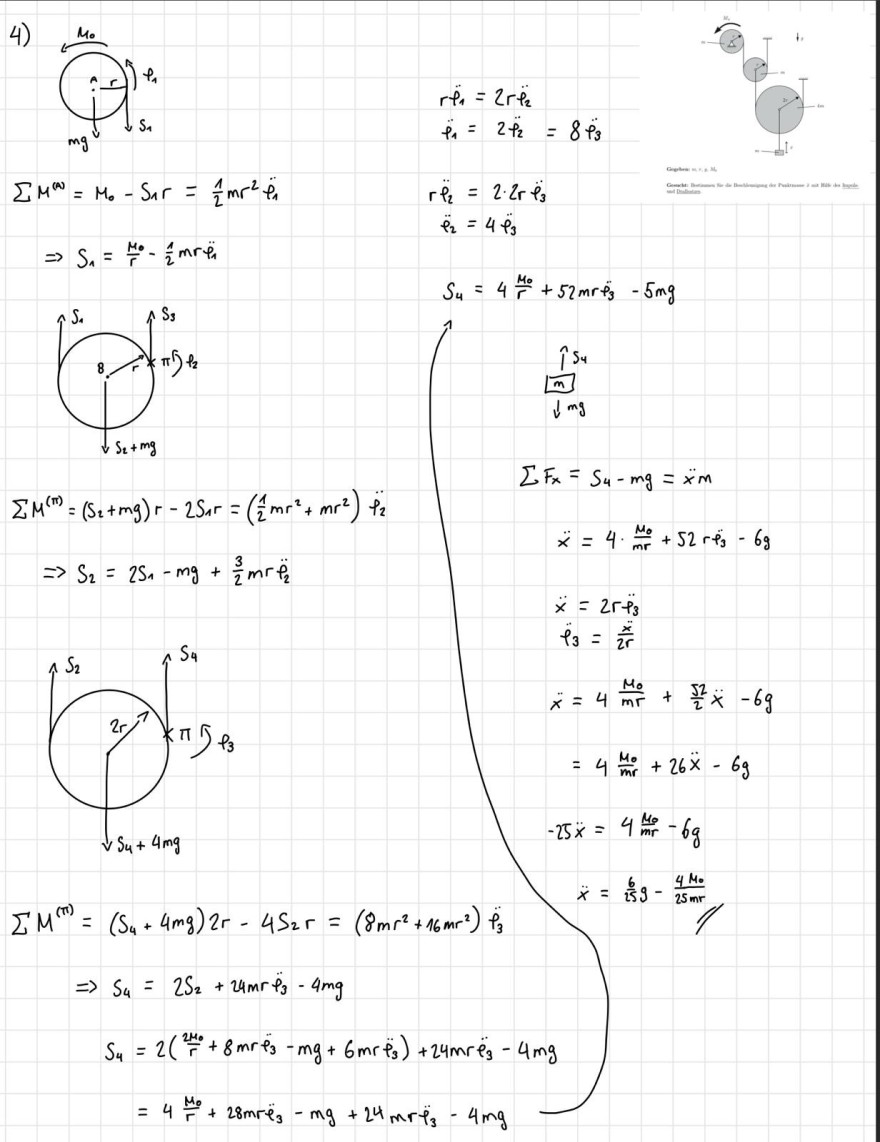
Aufgabe: Es soll die Beschleunigung der Punktmasse bestimmt werden
Text erkannt:
4)
\( - \)
\( \begin{array}{l} r \ddot{\varphi}_{1}=2 r \ddot{\varphi}_{2} \\ \ddot{\varphi}_{1}=2 \ddot{\varphi}_{2}=8 \ddot{\varphi}_{3} \end{array} \)
\( \begin{array}{l} \sum M^{(N)}=M_{0}-S_{1} r=\frac{1}{2} m r^{2} \ddot{\varphi}_{1} \\ \Rightarrow S_{1}=\frac{M_{0}}{r}-\frac{1}{2} m r \ddot{\varphi}_{1} \end{array} \)
\( r \ddot{\rho}_{2}=2 \cdot 2 r \ddot{\rho}_{3} \)
\( \ddot{e}_{2}=4 \ddot{e}_{3} \)
\( S_{4}=4 \frac{\mu_{0}}{r}+52 \mathrm{mr} \tilde{\rho}_{3}-5 \mathrm{mg} \)
\( \sum M^{(m)}=\left(S_{2}+m g\right) r-2 S_{1} r=\left(\frac{1}{2} m r^{2}+m r^{2}\right) \ddot{p}_{2} \)
\( \hat{p}_{\downarrow \mathrm{mg}}^{\hat{s}} \)
\( \Rightarrow S_{2}=2 S_{1}-m g+\frac{3}{2} m r \ddot{p}_{2} \)
\( \begin{aligned} \sum F_{x} & =S_{4}-m g=\ddot{x} m \\ \ddot{x} & =4 \cdot \frac{\mu_{0}}{m r}+52 r \ddot{e}_{3}-6 g \end{aligned} \)
\( \begin{array}{l} \ddot{x}=2 r \ddot{\rho}_{3} \\ \ddot{\rho}_{3}=\frac{\ddot{x}}{2 r} \end{array} \)
\( \begin{aligned} \ddot{x} & =4 \frac{\mu_{0}}{m r}+\frac{52}{2} \ddot{x}-6 g \\ & =4 \frac{\mu_{0}}{m r}+26 \ddot{x}-6 g \end{aligned} \)
\( -25 \ddot{x}=4 \frac{M_{0}}{m r}-6 g \)
\( \ddot{x}=\frac{6}{25} g-\frac{4 \mu_{0}}{25 \mathrm{mr}} \)
\( \begin{aligned} \Sigma M^{(\pi)}= & \left(S_{4}+4 m g\right) 2 r-4 S_{2} r=\left(8 m r^{2}+16 m r^{2}\right) \ddot{\rho}_{3} \\ \Rightarrow S_{4} & =2 S_{2}+24 m r \ddot{\rho}_{3}-4 m g \\ S_{4} & =2\left(\frac{2 \mu_{0}}{r}+8 m r \ddot{\rho}_{3}-m g+6 m r \ddot{\rho}_{3}\right)+24 m r \ddot{\rho}_{3}-4 m g \\ & =4 \frac{\mu_{0}}{r}+28 m r \ddot{\rho}_{3}-m g+24 m r \ddot{\rho}_{3}-4 m g \end{aligned} \)