Aufgabe:
Folgende Aufgabe. Die Berechnungen sollten stimmen. Jedoch ist meine Frage nun was genau denn Wv12= 34000kJ heißt. Ich habe mein Antwortsatz rot markiert. Stimmt der soweit? 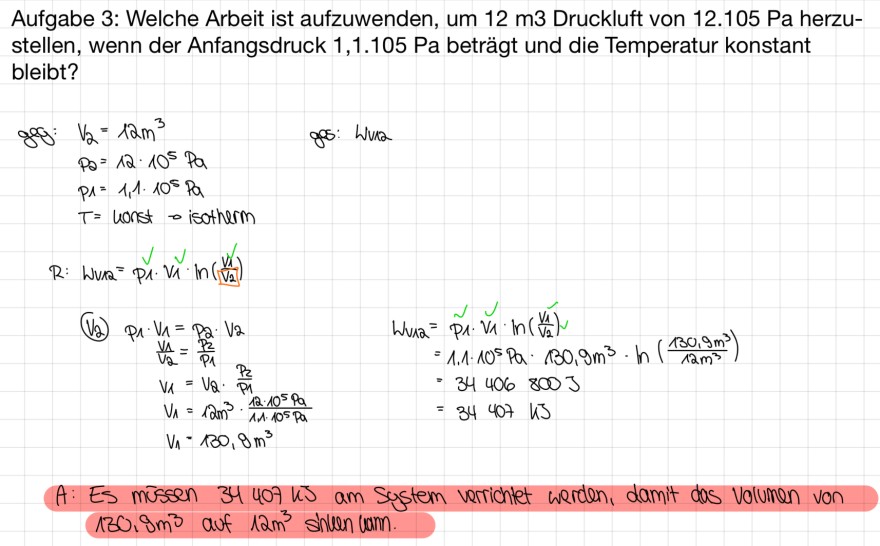
Text erkannt:
Aufgabe 3: Welche Arbeit ist aufzuwenden, um 12 m3 Druckluft von 12.105 Pa herzustellen, wenn der Anfangsdruck 1,1.105 Pa beträgt und die Temperatur konstant bleibt?
\( \begin{array}{l} V_{2}=12 \mathrm{~m}^{3} \\ P_{2}=12 \cdot 10^{5} \mathrm{~Pa} \\ P_{1}=1,1 \cdot 10^{5} \mathrm{~Pa} \\ T=\text { honst } \rightarrow \text { isotherm } \end{array} \)
gos: Wura
\( R: \omega_{V / 2}=p_{1} \cdot v_{1} \cdot \ln \left(\frac{v_{1}}{v_{2}}\right) \)
(V)
\( \begin{aligned} P_{1} \cdot V_{1} & =P_{2} \cdot V_{2} \\ \frac{V_{1}}{V_{2}} & =\frac{P_{2}}{P_{1}} \\ V_{1} & =V_{2} \cdot \frac{P_{2}}{P_{1}} \\ V_{1} & =12 \mathrm{~m}^{3} \cdot \frac{12 \cdot 10^{5} P_{2}}{11 \cdot 10^{5} P_{1}} \\ V_{1} & =130,8 \mathrm{~m}^{3} \end{aligned} \)
\( \begin{aligned} W_{V_{12}} & =\tilde{p}_{1} \cdot V_{1} \cdot \ln \left(\frac{V_{1}}{V_{2}}\right) \\ & =1.1 \cdot 10^{5} \mathrm{~Pa} \cdot 130,9 \mathrm{~m}^{3} \cdot \ln \left(\frac{130,9 \mathrm{~m}^{3}}{12 \mathrm{~m}^{3}}\right) \\ & =34406800 \mathrm{~J} \\ & =34407 \mathrm{~kJ} \end{aligned} \)
A: Es müssen 34407 kJ am Sustem verrichlet werden, damit dos volumen von \( 130.9 \mathrm{~m}^{3} \) auf \( 12 \mathrm{~m}^{3} \) sinlen lamm.