Berechnung Geschwindigkeit für Prüfung

Question

Aufgabe:

Problem/Ansatz:

Text erkannt:

PRÜFUNGSAUFGABEN - BERECHNUNG GESCHWINDIGKEIT

2015-7.4.1
Jahrlich wird ein Rennen mit selbstgebauten Pappbooten durchgeführt. 2014 benötigte der Sieger für die Wettkampfstrecke 2 Minuten und 1 Sekunde.
Berechnen Sie die Durchschnittsgeschwindigkeit des Siegerbootes in \( \frac{\mathrm{m}}{\mathrm{s}} \).
2016-75.4
Unalle werden auch durch die Nutzung von Smartphones verursacht. Wer als Fahrer auf das Display sieht, fährt in dieser Zeit ohne Blick auf die Straße. Während der Fahrt mit einer Geschwindigkeit von \( 100 \frac{\mathrm{~km}}{\mathrm{~h}} \) schaut ein Fahrer 2 s auf das Display. Berechnen Sie den dabei zurückgelegten Weg.

2019-Aufgabe 3
Der Triathlon ist eine der größten sportlichen Herausforderungen für Extremsportler. Bei der Weltmeisterschaft - dem Ironman auf Hawaii - belegte Patrick Lange 2018 den ersten Platz. Jeder Teilnehmer muss zuerst \( 3,8 \mathrm{~km} \) schwimmen, dann 180 km Rad fahren und schließlich \( 42,2 \mathrm{~km} \) laufen. Patrick Lange benötigte insgesamt 7 Stunden, 52 Minuten und 39 Sekunden. Seine durchschnittliche Geschwindigkeit beim Schwimmen betrug \( 4,5 \frac{\mathrm{~km}}{\mathrm{~h}} \). Die Radstrecke legte er in 4 Stunden und 29 Minuten zurück.
31. Berechnen Sie die Zeit, die Patrick Lange für die Schwimmstrecke benötigte.
3. Berechnen Sie die Durchschnittsgeschwindigkeit für die Radstrecke.
3.3 Der Bewegungsverlauf des Wettkampfes wurde in einem \( s(t) \)-Diagramm dargestellt.

Entscheiden und begründen Sie, welches Diagramm dem Bewegungsablauf näherungsweise entspricht.

A

2017-Aufgabe 7 siehe Rückseite

Zusatzaufgaben:
1) Berechne die Geschwindigkeit der Spitze des Minutenzeigers einer Turmuhr, wenn der Zeiger 2 m lang ist.
2) Anna fährt mit ihrem Mountainbike mit einer Geschwindigkeit von \( 36 \frac{\mathrm{~km}}{\mathrm{~h}} \). Berechne die Anzahl der Umdrehungen, wenn das Rad einen Durchmesser von 70 cm hat.

Answer 1

hallo, brauchst du nur einen Tipp für Aufgabe 3.3 ?

Im s/t-Diagramm gilt, je steiler der Graph, desto höher ist die Geschwindigkeit. Schwimmen ist am langsamsten, Radfahren am schnellsten und Laufen liegt dazwischen. Damit kann nur a die Lösung sein.

Im Detail:

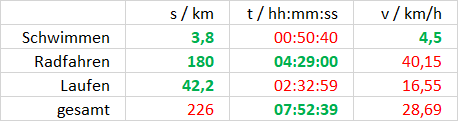
grün ist gegeben, rot kannst du berechnen.

Bei Unklarheiten bitte melden.

Comments

Das ist fantastisch, die 2 zusatzaufgaben bereiten mir auch Schwierigkeiten, das andere hab ich berechnet. Vielen lieben Dank

---

Zusatzaufgaben:

1.

der Zeiger ist 2 m lang, damit haben wir den Radius. Die Spitze des Zeigers beschreibt einen Kreis im dem Umfang 2·π·r ≈ 12,566 m. Der Minutenzeiger macht diese Kreisbewegung in einer Stunde. Jetzt kannst du die Geschwindigkiet ausrechen.

2.

das Rad einen Umfang von 70 cm·π ≈ 220 cm ≈ 2,2 m ; weiterhin sind 36 km/h = 10 m/s ; jetzt rechnest du Geschwindigkeit durch Umfang, also mach das Rad 4,55 Umdrehungen/s

---

Zusatz 1 habe ich 0,00349 m/s raus.

---

Ach nee es sind 0,21 m/s

---

zeig 'mal, was du gerechnet hast.

---

Text erkannt:

Zuack(1)
\( \text { geg: } \begin{aligned} x & =2 \mathrm{~m} \\ z & =60 \mathrm{~min}=3.600 \mathrm{~s} \end{aligned} \)
geo. Geochwindigheit \( =v \) in \( \mathrm{m} / \mathrm{s} \)
Los:
\( \begin{array}{l} 2 \cdot \pi \cdot r \\ 2 \cdot \pi \cdot 2 m \approx 12,566 \mathrm{~m} \\ 12,566 \mathrm{~m}=1 \mathrm{~h} \\ 0 / 00349 \mathrm{mlsg} \\ v=\frac{s}{t} \\ v=\frac{12,566}{60} \\ v=\text { dooot4s } \mathrm{mu} / \mathrm{s} \\ V=0,21 \mathrm{~m} / \mathrm{s} \end{array} \)

---

die Geschwindigkeit ist 12,566 m/h. Du hast die Zeit in Minuten angesetzt, die Geschwindigkeit ist dann 0,21 m/min ; deine 0,00349 ist die Geschwindigkeit in m/s.

---

Ah okay danke