Hallöchen,
Ich habe folgendes Problem:

Text erkannt:
Rakete. Eine Rakete hat die Startmasse \( m_{0}=2,5 \times 10^{5} \mathrm{~kg} \) und den zeitlich konstanten Massenausstoß \( \dot{m}=1000 \frac{\mathrm{kg}}{\mathrm{s}} \). Die Ausströmgeschwindigkeit der Gase ist \( u=3,0 \frac{\mathrm{km}}{\mathrm{s}} \).
a) Berechnen Sie den Zeitpunkt \( t_{1} \) nach dem Start, zu dem der gesamte Brennstoff verbraucht ist und die Rakete nur noch eine Endmasse \( m_{1}=3,0 \times 10^{4} \mathrm{~kg} \) hat.
b) Berechnen Sie die Beschleunigung \( a_{0} \), mit der die Rakete abhebt.
Um das Problem zu lösen hab ich die Ziolkowski Gleichung gegeben und dessen Herleitung. Trotzdem ist mir die Herangehensweise der Aufgabe unklar, wenn der Massenausstoß gegeben ist. Vielleicht komme ich durcheinander, aber die Formel für den Massenausstoß steht so nicht in der Herleitung, weshalb ich mit der Info nichts anfangen kann.
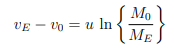
Danke im Voraus für jegliche Anregungen :)