Bahngeschwindigkeit und Winkelgeschwindkeiten in Physik

Question

Wir haben uns aufgeschrieben:

Bahngeschwindigkeit

v=s/t=2*pi*r/ T

Die Bahngeschwindigkeit gibt die Geschwindkeit eines Punktes auf der Kreibahn mit dem Radius r.

> Winkelgeschwindigkeit

w=2*pi/T

Die Winkelgeschwindigkeit w gibt an, wie schnell ein ,,Zeiger" den Winkel Phi überstreicht.

Ich verstehe leider den Unterschied zwischen den beiden Geschwidkeiten  nicht genau. Mathematisch gesehen spielt der Radius bei der Winkelgeschwindigkeit nur eine Rolle.

Was ich so bei der Bahngeschwidkeit verstanden habe ist: Wenn ein Körper eine Drehbwegung macht, befindet er sich auf einer Kreisbahn. Und er besitzt natürlich eine Geschwindigkeit. Und diese G. heißt Bahngesch.

Die Winkelgeschwidkeit verstehe ich überhaupt nicht. Man hat das uns mit einerUhr versucht zu erklären (=habe es aber vergessen) ... Und wieso der Winkel Ph?

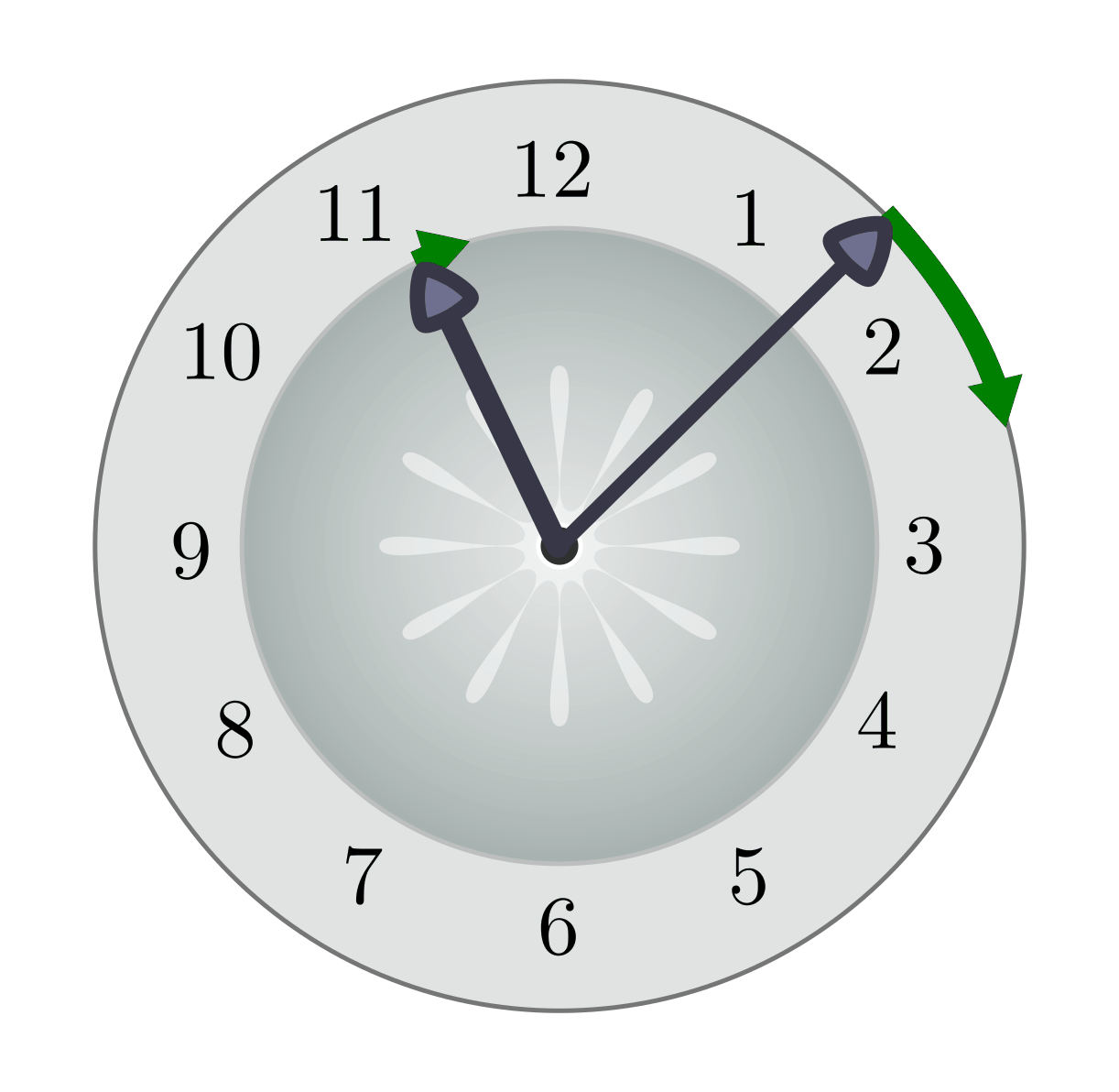
Kann man das so erklären:
Bsp wir hätten noch einen dritten Zeiger. Der Zeiger beginnt bei dem "zeiger bei 11Uhr" und er bewegt sich bis zum Zeiger bei 1 1/2 Uhr...

Das ist die Geschwidgkeit die der ZEiger für diesen Winkel braucht?

Answer 1

Vielleicht hilft dir diese Erklärung:

Winkelgeschwindigkeit ist sowas wie Drehzahl, Umdrehungen pro Sekunde.
Der Winkel für eine Umdrehung ist 2pi, die Winkelgeschwindigkeit 2pi/T,
T ist darin die Zeit für einen Umlauf, die Periodenzeit. Die Einheit für
die Winkelgeschwindigkeit ist 1/s.

Bahngeschwindigkeit ist die Geschwindigkeit der Bewegung entlang einer Bahn,
gerade oder gekrümmt, in Metern pro Sekunde, die Einheit also m/s.

Bei einer kreisförmigen Bahn ist die Länge pro Umlauf 2pi*r, die Bahngeschwindigkeit v
kann hier aus der Winkelgeschwindigkeit w berechnet werden als v = w*r, und
umgekehrt w = v/r.

Warum 2 phi?

Der Umfang eines Kreises mit dem Radius 1 (Einheitskreis) beträgt genau 2 π.

Die Formel für den Umfang eines Kreises lautet ja U = 2π * r. Wenn du für r = 1 setzt, kommst du zu U = 2π.

Comments

Danke aber wieso muss man bei der Winkelgeschwidkeit für r=1 einsetzen.

---

Man benutzt einen vollständigen Umlauf (2 π ) pro benötigter Zeit eines kompletten Umlaufs ( T ).

Deshalb die Formel zur Berechnung der Winkelgeschwindigkeit

ω = ( 2π ) / T

Ein Beispiel: Die Umlaufzeit der Erde um die Sonne beträgt 3,1558*10⁷s. 

Die Winkelgeschwindigkeit der Erde errechnet sich somit aus

ω = (2π) / 3,1558*10⁷s.

Merke dir : Gradmaß: 360°, Bogenmaß: 2π

Answer 2

Die Winkelgeschwindigkeit gibt an, welchen Winkel (im Bogenmaß) die "Radiusstrecke" 

vom Kreismittelpunkt zum Körper pro Sekunde (oder auch in einer anderen Zeiteinheit)

 "überstreicht". In der Zeit T überstreicht sie den Bogenmaßwinkel 2π (= 360°)

Wenn zum Beispiel ein Satellit bei seiner Umlaufbahn immer über dem gleichen Punkt 

der Erde bleibt  ("geostationär"), hat er die gleiche Winkelgeschwindigkeit wie der Punkt 

auf der Erdoberfläche bei der Erddrehung, aufgrund des größeren Bahnradius aber eine 

höhere Bahngeschwindigkeit, weil er bei jedem Umlauf eine größere Strecke

zurücklegt.