[PHYSIK] Cosinussatz anwenden bei Kräfteaddition ( Berechne FR Mit F1 = 30N, F2 = 40N )

Question

Hallo zusammen,

ich hänge an einem Problem was ich nicht lösen kann. Es geht um die Winkelfunktion "Sinussatz".

In der Schule haben wir eine Aufgabe, die hieß:

"Geg:

F1 = 30N

F2 = 40

α = 30°

Berechnen Sie FR (F Resultierende).

Ja, soweit alles okay. Man kann einmal Grafisch diese Sache erledigen.

Skizziert würde das so aussehen:

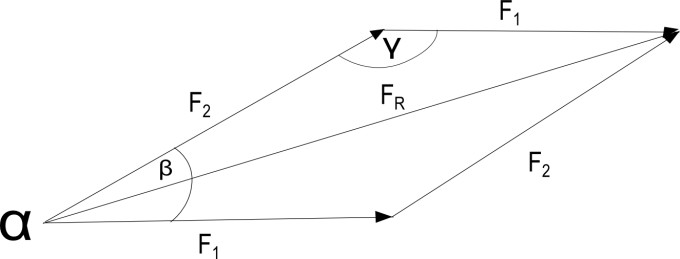
Jetzt zu meiner Frage:

Wie kann es sein, dass man auf diese Formel kommt?

$$ { F }_{ R }\quad =\quad \sqrt { { F }_{ 1 }^{ 2 }+{ F }_{ 2 }^{ 2 }\quad +\quad 2*{ F }_{ 1 }{ F }_{ 2 }\quad cos\quad \sphericalangle ({ F }_{ 1 },{ F }_{ 2 }) }  $$

Die Formel ansich ist okay. Aber der Winkel am Ende, wieso cos(α) ?

Und wie kann es sein, dass man dann direkt FR rausbekommt?

Liebe Grüße

Answer 1

Für die resultierende Kraft Fr wird der Cosinussatz benutzt !

Einfach mal anschauen .

Answer 2

Es gilt

cos(Alpha) = - cos(180° - Alpha)

https://www.matheretter.de/wiki/einheitskreis

Betrachte zur Erklärung dieses Video:

Answer 3

Die Sachlage stellt sich zunächsr einmal so dar

Zu ermitteln ist der in deiner Formel bezeichnete
Winkel ( F1,F2 ) oder gamma zu 150 °

Der cosinussatz lautet
( siehe http://de.wikipedia.org/wiki/Kosinussatz )

c^2 = a^2 + b^2 + 2*a*b * cos ( gamma )

c^2 = 30^2 + 40^2 + 2*30*40 * cos (150 )

Daraus noch für beide Seiten die Wurzel ziehen.