Hallo, wie kann ich hier a berechnen, welche Formel muss ich anwenden?
Aufgabe:
Das Potential eines elektrischen “Punktdipols” mit Wert p und Richtung entlang der x-Axis eines kartesischen Koordinatensytems ist: ∅(r) = (1/4πε0 )*(p*r/r3 )
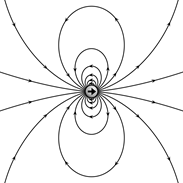
Schematische Abbildung der Feldlinien von E
a) Berechne die Komponenten Ex , Ey , Ez
des dazu gehörigen elektrischen Feldes E.
b) Berechne die Divergenz des Feldes ∇*E