Winkel bestimmen, um größte Masse zu transportieren

Question

habe Probleim beim Ansatz der Aufgabe.

Eine mit Sand gefüllte ruhende Kiste soll an einem Seil gezogen werden. Die Zugkraft darf 1100N nicht
übersteigen. Die Haftreibungszahl zwischen Boden und Kiste betrage μH=0,35

Wie muss der Winkel zwischen der Horizontalen und dem Seil gewählt sein, damit man die
größtmögliche Menge an Sand transportieren kann?

Ich habe die gleichungen aufgestellt:

0 = F * cos(a) - Fh

0 = - Fg + Fn + F * sin (a)

weiter weiß ich nicht. was ich machen soll

Answer 1

Hier meine Überlegungen

Zunächst dachte ich Skizze 1 wäre zutreffend

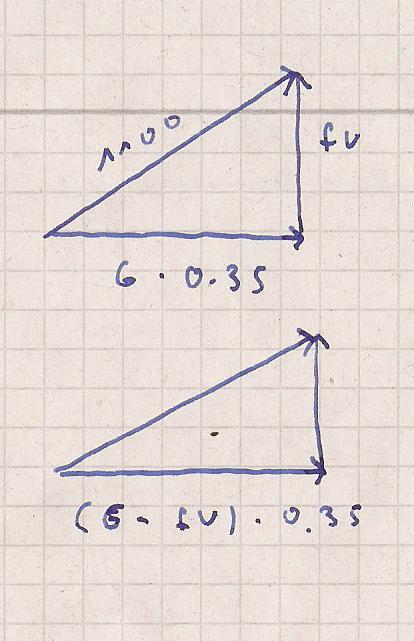
Haftkraft = [  F(N) oder G(ewicht)  ] * 0.35

Die Zugkraft im Seil erzeugt eine Kraft F ( vertikal ) die auf das Gewicht
enlastend wirkt. Deshalb komme ich zu Skizze 2.

Nun folgt die Anwendung des Pythagoras
1100^2 = fv^2 + [ ( G - fv ) * 0.35 ]^2

Unter Benutzung eines Matheprogramms habe ich nach G umgestellt:
und erhalte G ( fv ) = ... ellenlange Formel

G ist dann eine Funktion von fv. Gesucht wird das Maximum von G.
Also 1.Ableitung bilden und den Extremwert berechnen.
fv =  363.39 N
sin ( α ) = fv / 1100
α = 19.29 °

fh^2 + fv^2 =1100^2
fh = 1038.24 N

fh = ( G - fv ) * 0.35
1038.24 = ( G - 363.39 ) * 0.35
G = 3329.79 N

Wenn ich mich nicht irre ( Sam Hawkins )