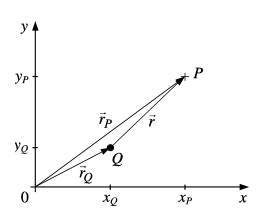
Gegeben ist eine Punktladung Q am Ort (x_Q, y_Q)
Berechnen Sie die Komponenten E_x und E_y der elektrischen Feldstärke E im Punkt(x=x_p, y =y_p)
Im Punkt P liege eine Probeladung q. Welche Kraft F wirkt auf q?
Für die Koordinaten soll dabei gelten: x_p= 4a, x_Q= 2a und y_P= 3a, yQ=a .