ich werde mal versuchen einen Anfang zu machen. Bei vielen Konstruktionen muss man zunächst Annahmen treffen und dann auf Grund dieser Annahmen prüfen, ob die geforderten Bedingungen (z.B. Festigkeiten) erfüllt werden. Trifft das dann nicht zu, so variiert man die Annahmen bis sich ein - unter den gegebenen Umständen - optimierter Entwurf heraus bildet.
So nehmen wir hier an, wir kennen den Wert für \(a\). Dann kann man zunächst die Kräfte bzw. Momente bestimmen. Ich habe ein Koordinatensystem gewählt, bei dem der Drehpunkt \(D\) im Ursprung liegt. Die X-Achse zeigt nach rechts und die Y-Achse nach oben (die schwarzen Geraden):
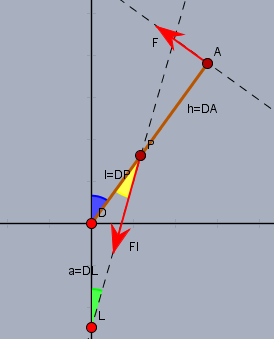
Um das Kräfte- bzw. Momentengleichgewicht aufzustellen, benötigt man die Position des Punktes \(P\) oder den gelben Winkel (s. Skizze). Das Momentengleichgewicht um \(D\) liegt vor, wenn
$$F \cdot h + F_l \cdot l \cdot \cos \beta \cdot \sin 16° - F_l \cdot l \cdot \sin \beta \cdot \cos 16° = 0$$
Wobei \(\beta\) der blaue Winkel ist. Der grüne Winkel ist mit \(16°\) gegeben. Eine Umformung macht daraus
$$F \cdot h - F_l \cdot l \cdot \sin(\beta - 16°) = 0$$
Der Winkel \(\beta - 16° = \alpha\) ist der gelbe Winkel im Punkt \(P\). Und dieser wiederum - bzw. sein Sinus - lässt sich über den Sinussatz im Dreieck \(LPD\) berechnen. Es ist
$$\frac{\sin \alpha}{ a} = \frac{\sin 16°}{l} \quad \Rightarrow \sin \alpha = \frac{a}{l} \sin 16°$$
Daraus folgt nun die Federkraft \(F_l\) in Abhängigkeit von \(a\)
$$F_l = \frac{h}{a \cdot \sin 16°} F$$
... womit Teilaufgabe 1 im Grunde erledigt wäre. Es wäre hilfreich, wenn Du jetzt konkrete Fragen stellen würdest.
Gruß Werner