Hallo Simon,
Das Torsionsträgheitsmoment ist nicht das Torsionswiderstandsmoment. Letzteres ist ein für mich unbekannter Ausdruck. Ich dachte mir aber schon, dass aus dieser Richtung der Wind weht! Aber bei Wikipedia steht auch (dahinter):
Für andere Geometrien der Fläche lässt sich das Torsionsträgheitsmoment meist nur numerisch berechnen.
Ich hatte Vorlesungen in Leichtbau und kann mich erinnern, dass es für bestimmte Profile auch analytisch möglich war; einfach war es aber nicht!
Weiter würde ich nicht etwas als 'falsch' bezeichnet, nur weil es von Lösungen im Script abweicht. Alle Modelle, die Du in deinen Vorlesungen lernst, sind ja nur Modelle, die unter idealen Voraussetzungen gelten. In der Praxis behilft man sich damit, indem man genug Sicherheit aufschlägt, oder mit heuristischen gewonnen Faktoren multipliziert (z.B. Kerbzahlen). Bedenke bitte, dass diese 'Rotationsrechnung' ja nur für die Schnittfläche der Schweißnaht gilt, aber weder davor noch dahinter (in der Richtung der Drehachse also senkrecht zur Zeichenebene gesehen). D.h. Du hast hier in Wirklichkeit einen hochgradig dreidimensionalen Spannungszustand. Man kann aber davon ausgehen, dass bei dieser Konstruktion die Schweißnaht das schwächste Glied in der Kette ist, und das das Versagen mit Sicherheit durch Abscheren auftritt.
IMHO ist das polare FTM eine gute Abschätzung und zwar weil die Naht dünn(!) ist. Betrachte dazu mal einen Ausschnitt der Naht:
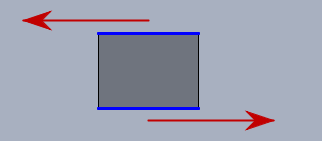
Das ist jetzt die Sicht von oben auf die Konstruktion! Das graue Rechteck sei eine kurze und dicke Schweißnaht (natürlich übertrieben dargestellt) an den blauen Seiten ist sie mit dem Material verbunden. Stellst Du hier die Kräftesumme auf, passt alles. Stellst Du aber die Momentensumme auf, so fehlt hier was! Du kannst nämlich auf diese Weise gar keine reine Schubspannung aufbringen; es fehlen die Kräfte an den Seiten, die das Moment aufnehmen, welches durch den Abstand der blauen Seiten zustande kommt. Das führt zu zusätzlichen Spannungen innerhalb des Materials, die in der Praxis u.U. schwer zu kalkulieren sind - und das ist IMHO auch im Prinzip der Unterschied zwischen dem polaren FTM und dem Torsionsträgheitsmoment. Macht man aber obiges Rechteck immer dünner, d.h. die blauen Seiten wandern immer weiter zusammen, schrumpft damit auch das Problem, da das 'störende Moment' immer kleiner wird!
Und genau das ist hier der Fall. Der Abstand der beiden Seiten ist quasi gleiche 0, wenn man mal von der Ausdehnung der Schweißnaht selbst absieht.
Sprich mal Deinen Dozenten darauf an, ob er/sie das genauso sieht oder eventuell ganz anders ;-)
Gruß Werner