Schiff soll mit Kraft F=120 kN nach rechts gezogen werden. Gleichungssytem erstellen und lösen

Question

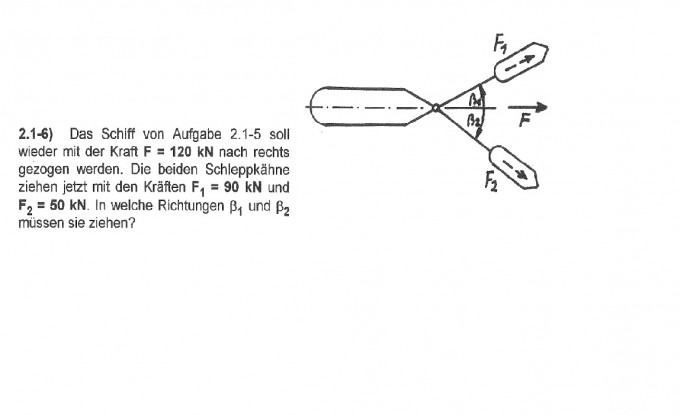
bitte die aufgabe zu lösen ich habe bis jetzt folgenden ansatz:

1) 0 = f1 * sin (ẞ1) - f2*sin(ẞ2)

2) 120 = f1 * cos (ß1) + f2 * cos (ẞ2)

aber jetzt weiß ich nicht mehr weiter mir ist klar das ich eine nach beta 1 umformen muss. bspw und dann beta 2 aus der zweiten nach beta 2 umgeformten gleichung in bsp. 1 einsetzten muss aber an der umsetzung habert es .

bitte vollständige Lösung angeben mit Schritten .

ps. die zeichnerische Lösung hab ich .

Comments

Hilft dir die 'solution': http://www.wolframalpha.com/input/?i=0+%3D+f+*+sin+%28B%29+-+g*sin%28A%29+%2C+120+%3D+f+*+cos+%28B%29+%2B+g+*+cos+%28A%29++

auf die Sprünge?

Answer 1

Wenn du ein Kräfteparallelogramm malst

könntest du erkennen das es da nur dem Cosinussatz und dem Sinussatz bedarf.

Die Schiffe ziehen in den Winkeln 42.83 und 22,19 Grad. Probier das mal nachzurechnen.

Comments

geht das nicht mit Gleichungssystem zu lösen ? ( auch wenn es komplizierter ist möchte ich es gerne wissen)

zum cosinus satz der lauter a ² + b ² - 2 ab * cos y

doch was beduetet dies in diesem konkretten fall

komm leider immernoch nicht weiter vielen dank für die tipps !

---

probier es mal kurz mit dem sinussatz den kann ich aber hilfter der mit zur kompl. Lösung ?

---

komm einfach nicht drauf sorry... hast du nen tipp ?

---

Zeig mir bitte beide Lösungen die mit dem Gleichungssystem und deine schnellere Lösung!

besten dank schonmal

---

Du brauchst den Kosinussatz um einen Winkel zu bestimmen

c^2 = a^2 + b^2 - 2·a·b·COS(γ)

γ = ARCCOS((a^2 + b^2 - c^2)/(2·a·b))

β1 = ARCCOS((90^2 + 120^2 - 50^2)/(2·90·120)) = 22.19

β2 = ARCCOS((50^2 + 120^2 - 90^2)/(2·50·120)) = 42.83

Du siehst. Eigentlich ist das recht simpel mit dem Cosinussatz.

---

danke hät ich das auch mit dem sinussatz oder mit einem gleichungssystem lösen können (s. meinen Ansatz) ?

---

Alleine mit dem Sinussatz nicht. Wenn man bei einem Dreieck alle 3 Seiten gegeben hat braucht man den Cosinussatz um den ersten Winkel auszurechnen. Danach kann man auch mit dem Sinussatz weiter machen. Mit einem Gleichungssystem geht das auch. Ist aber viel viel schwieriger. Du siehst ja was Wolframalpha da für ein Murks macht.

---

Könntest du das mal sauber mit dem Gleichungssystem lösen. Wäre interessant da das mein Ansatz war und ich mich iwie verzettelt habe damit! Ja das es mit dem sinussatz nicht geht leuchtet mir ein dafür braucht man min. 1 startwinkel.

---

In der Aufgabenstellung steht ja " löse mit einem Gleichungssystem ".

Vielleicht  könnte man den " trigonometrischen Pythagoras "
anwenden um z.B. den sin () in cos () zu verwandeln.
( sin a )^2 + ( cos a )^2 = 1
sin (a) = √ ( 1 - ( cos a )^2 )

1) 0 = f1 * sin ( ẞ1 ) - f2 * sin ( ẞ2 )
1) 0 = f1 * √ ( 1 - ( cos ß1 )^2 ) - f2 * √ ( 1 - ( cos ß2 )^2 )
und
2) 120 = f1 * cos (ß1) + f2 * cos (ẞ2)

Mein Matheprogramm hatte auch Schwiergkeiten.

Falls das eine Aufgabe ist die im Unterricht noch
besprochen wird würde mich die Lösung
mit Gleichungsssystem auch interessieren.

---

Der Kommentar wurde in eine Antwort umgewandelt.

---

In komplexen Zahlen (schreibt sich etwas schneller als mit sin und cos, ist aber im Prinzip dasselbe) hast du  F1=a+bi und F2=c+di  und die Gleichungen  F1 + F2 = 120,  also a+c = 120 und b+d = 0 (die stehen ja schon in der Fragestellung) sowie  a^2 + b^2 = 90^2  und  c^2 + d^2 = 50^2 . Quadrieren der ersten beiden Gleichungen und Addition liefert  90^2 + 2·(ac+bd) + 50^2  =  120^2 , also  ac+bd = 1900 . Einsetzen der ersten beiden Gleichungen führt auf (120-c)·c - d^2 = 1900  und somit  120c = 1900+50^2 , also  c = 110/3 , damit weiter a = 250/3  und schließlich  b = √( 90^2 - a^2 )  = 20/3 · √26  sowie   d = -20/3 · √26 . Letztlich erhält man  tan β1 = b/a = 2/25· √26  und  tan β2 = d/c = -2/11· √26

---

@ georgborn:

"In der Aufgabenstellung steht ja " löse mit einem Gleichungssystem "."

Die Äußerung kam nur vom Fragesteller und steht in der Aufgabe nicht drin. Dein zweiter Ansatz ist recht schön. Auch hier ein Dreieck gegeben. Durch Aufteilung über h erhällt man zwei rechtwinklige Dreiecke.

---

Richtig. Die Forderung nach einem Gleichungssystem kam vom 
Fragesteller.

Auch dort ( bei deiner Antwort ) bedarf es eigentlich keines
Gleichungssystems.

Meine Antwort basiert auf 2 Gleichungen mit 2 Unbekannten.
Üblicherweise wird so etwas als Gleichungssystem  bezeichnet.

---

Ja. War ein kleiner Denkfehler von mir. Du hast natürlich völlig recht.

---

Halb so wild . Hier zu Erheiterung noch etwas Lustiges
oder  " so kann man es auch drehen. "

Ungarn Anfang des letzten Jahrhunderts. Ein älteres Unternehmer-Ehepaar
liegt abends im Bett. Der Mann dreht sich von einer Seite auf die
andere und kann nicht schlafen.

  Die Frau richtet sich auf, knipst das Licht an und fragt " Mann, was hast du ? ".

  " Ich muß morgen zum Bankdirektor gehen und im sagen das
ich den großen Kredit, der morgen fällig wird, nicht zurückzahlen
kann. " Die Frau überlegt etwas und zeigt dann auf das Telefon und sagt

  " Dort steht das Telefon. Du rufst den Bankdirektor jetzt an und sagst
ihm das du den Kredit nicht zurückzahlen kannst. Dann kann er
nicht schlafen und wir haben unsere Ruhe. "

Answer 2

Eine Lösung mit Gleichungssystem fiel mir doch
noch ein

Comments

Super Ansatz georgborn! hab mich mal hineingedacht und das GL-System versucht aufzulösen leider komm ich zu einen falschen Ergebnis da p ( kenn das mit q , p aus der schule ) größer wie die hpotenuse ibitte um Hilfe weitere Tipps.

---

Dies ist nur ein Fülltext

---

Super hab auch meinen Fehler gefunden danke für alle die sich beteiligt haben .