Statik: Lagerkräfte/ Schnittreaktionen in einfachem Montagekran

Question

Hallo,

der Kran ist unten mit 4 Rollen gelagert, die vorderen sind fest gelagert (also im Bild links), die hinteren lose. Die Rollen befinden sich unten auf einem geschweißten Rechteckrahmen, der dann únten in der Mitte des Gestells (im Bild rechts) zusammengeführt wird. ´

Mir geht es zunächst nur um das Grundgestell und die Rollen. Ich habe ja unten durch die 4 Rollen schon 6 Unbekannte. Die zwei Umlenkrollen am Rahmen oben liefern ja auch 4 weitere Unbekannte. Also sind es insgesamt 10 Unbekannte.

Eingeprägte Kräfte ist eine Last von 15000 Newton am Haken und die Gewichte der Windeeinheit (2). Die würde ich dann später selber in die Berechnung einbauen.

Mir geht es zunächst darum, wie ich grob vorgehen muss, um an die Lagerkräfte zu kommen. Ich hab mich bis jetzt nur mit Statik in der Ebene beschäftigt und nícht in 3D.

Ich hoffe, mir kann jemand ein paar Tipps geben. Zum Beispiel wie viele Gleichungen mir überhaupt zur Verfügung stehen und wie die Freikörperbilder aussehen. Danke!

Comments

Hallo Simon,

die Anzahl der Unbekannten (Kräfte) hängt auch davon ab, was Du überhaupt berechnen möchtest. Wenn  es nur um die Kraft in den Rollen geht, auf denen der Kran verfahren wird, so kanst Du u.a. die Lagerrollen des Seil ignorieren und annehmen, dass die Last fest am Kran montiert ist. Was genau ist der Unterschied zwischen einer fest gelagerten und einer lose gelagerten Rolle?

Und 3D ist hier wie 2D - nur eine Dimension mehr. Hört sich erstmal ein wenig zu einfach an, ist aber so. Auch in 2D betrachtest Du 2 Koordinatenrichtungen jeweils getrennt (Summe aller Kräfte usw.). Genauso geht das in 3D - statt Kräftesummen in zwei Richtungen stehen Dir hier Kräftesummen in drei Richtungen zur Verfügung. Und statt Momente senkrecht zur Zeichenebene in 2D gibt es in 3D Momente senkrecht zu allen drei Koordinatenachsen; mit entsprechend mehr Unbekannten.

Wirkt die Kraft (Gewichtskraft der Last) nur nach unten, so reicht es auch in 3D aus nur die Kräftesumme in vertikaler Richtung und die Momentensumme um eine horizontale Achse zu bestimmen. Vorausgesetzt es gibt keine signifikanten Änderungen bzw. Asymmetrien in  der 'Tiefe' - also hier senkrecht zur Zeichenebene. Darüber hast Du aber keine Angaben gemacht.

Wichtig ist: welche Kräfte bzw. Belastungen sollen berechnet werden?

---

Hallo,

es sollen sowohl Kräfte in den Rollen (unten und oben) als auch die schnittreaktionen im gesamten Rahmen berechnet werden.

Das ist eine Konstruktionsübung im 3. Semester Maschinenbau und man soll zunächst mit den Lagerkräften anfangen :)

Losgelagert heißt das ich den Kran eben hinten nach links und rechts bewegen kann, das die entsprechenden Lager dann eben nur eine Kraft aufnehmen.

Unser Problem ist, dass wir z. B. nicht wissen wie man oben die Lagerkräfte in der Rolle beim Haken berechnet bzw. das System korrekt freischneidet und ob/wie diese Lagerkräfte dann auf den Träger oben übertragen werden.

Vielleicht hast du da ein paar Tipps für uns. Du gibst ja immer sehr gut verständliche Antworten :)

---

Hallo Simon,

ich habe gerade auch einige Probleme bei dieser Übungsaufgabe. Hast du noch die Lösungen zu dieser Aufgabe? Ich würde mir gerne ein mal die Zeichnungen anschauen, da ich dort nicht ganz so fit bin.

---

Hallo Simon,

wie es der Zufall will haben meine Gruppe und ich die identische Aufgabe bekommen. Ich hätte eine Frage an dich, wenn es geht würde es mich freuen, wenn du mich kontaktieren würdest unter der Email: Vanessa.preiske@yahoo.de

Liebe Grüße

Vanessa

Answer 1

Hallo Simon,

Du schriebst: "Unser Problem ist, dass wir z. B. nicht wissen wie man oben die Lagerkräfte in der Rolle beim Haken berechnet bzw. das System korrekt freischneidet und ob/wie diese Lagerkräfte dann auf den Träger oben übertragen werden."

Nun - das ist relativ einfach. Die Rolle brauchst Du nicht freischneiden. Im Allgemeinen wirkt die Kraft nur senkrecht zur Achsrichtung des Lagers, wenn die Rolle so belastet wird, wie man sich das für eine Seilrolle vorstellt. Die Reibung sollte bei derartigen Konstruktionen zu vernachlässigen sein. Folglich treten im Lager keine Momente in Richtung der Achse auf und der Betrag der Seilkraft ist überall gleich.

Mit diesen Annahmen kann man also mit Kenntnis der Seilkraft sofort die Kräfte bestimmen, die die Lager der Rollen auf das Gestell ausüben. Oben im Bild ist \(S\) die Seilkraft, deren Betrag überall identisch der Last ist (rote Pfeile). Die grünen Kräfte ist die jeweilige Summe der beiden Seilkräfte an jeweils einem Rollenlager. Die Richtung der Kräftesummen zeigt jeweils in Richtung der Winkelhalbierenden der ein- und auslaufenden Seilrichtung. Die Beträge dieser Kräfte sind wichtig für die Auslegung der Lager. Für das was noch kommt, reichen die Komponenten der Kräfte aus.

Wichtig ist die Auslegung am Punkt \(X\). Dies ist sicher eine der Stellen mit der größten Belastung im Gestell. Ebenso die untere Ecke des Gestells. Diese Punkt sollte man freischneiden:

Die blau eingezeichneten Kräfte \(F_x\) und \(F_z\) und das Moment \(M_y\) sollen die Reaktionskräfte des senkrechten Ständers auf den Ausleger mit den Rollen sein. Jetzt wie gehabt Kräfte- und Momentensumme aufstellen und man kann diese Kräfte bzw. das Moment berechnen. Wobei man hier sieht, dass es von Vorteil sein kann, die wirkenden Kräfte (rot) gleich als ihre Komponenten zu belassen.

Da ich nicht weiß, wie tief ich hier in Erklärung einsteigen muss/soll, beende ich das hier zunächst. Bitte fragt nach, wenn noch etwas unklar ist. Ich bin voraussichtlich morgen Abend wieder online.

Gruß Werner

Comments

Hallo Werner,

Danke für die Antwort!

Ein paar Fragen habe ich noch. Die Kräfte im Lager wo du rot markiert hast, könnten die auch in die andere Richtung zeigen? Man würde ja erwarten, da ja die Zugkraft im Seil nach rechts zeigt, dass dann die Lagerkraft nach links zeigt (bei A1). Und din Richtung der Kräfte im Lager gelten dann auch für das Gestell, oder muss man actio=reactio beachten, also die Richtung der Lagerkräfte umdrehen, wenn man das Gestell betrachtet?

Würde man für die schnittreaktionen oben dann 3 Bereiche brauchen? Also von 0-A1, dann von A1-A2 und dann von A2-X?

Eine letzte Frage zur Dimensionierung habe ich noch :)

Angenommen ich kenne jetzt alle Schnittreaktionen. Nächster Schritt ist ja dann die Berechnung der größten Momente und Spannungen. Die Querkräfte bei den Schnittreaktionen erzeugen ja Torsionsspannungen und die Momente Biegespannungen, die ich dann mit den Normalspannungen verrechnen kann. Tut man anschließend die Normal und Torsionsspannungen in eine Vergleichsspannung umrechnen? Ziel soll ja sein,  z. B. die Dicke des Trägermaterials zu bestimmen. Allerdings brauche ich die ja schon für die Berechnung der Flächenträgheitsmomente bei der Biegrspannung.

Es wäre schön, wenn du kurz zu meinen Gedanken wegen der Dimensionierung was sagen könntest bzw. wie wir anders rangehen sollen. Danke!

LG

Simon

---

Hallo Simon,

Du schriebst: "Die Kräfte im Lager wo du rot markiert hast, könnten die auch in die andere Richtung zeigen? Man würde ja erwarten, da ja die Zugkraft im Seil nach rechts zeigt, dass dann die Lagerkraft nach links zeigt"

Ich begann oben "Die Rollen brauchst du nicht frei schneiden ...". Die roten Kräfte, die ich eingezeichnet habe, sind die Kräfte die die Rollen auf ihre Lager ausüben und nicht umgekehrt!

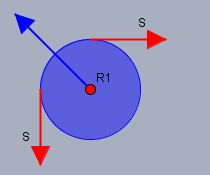
Wenn ich die Rolle frei schneide, so führe ich eine neue Kraft ein (hier die blaue), welche die Kraft darstellt, die das Lager auf die Rolle ausübt. Die grüne Kraft in meiner Antwort oben (erste Skizze) ist dann nach actio=reactio die Gegenkraft mit umgekehrtem Vorzeichen.

Grundsätzlich sollte man versuchen, die Kräfte in der Richtung zu zeichnen, in der sie voraussichtlich auch wirken - das ist besser für die Anschauung. Rein formal wäre es egal, da Kräfte auch negativ werden können. Nur eine einmal gewählte Richtung muss natürlich durchweg beibehalten werden.

Du schriebst: "Rechnet man anschließend die Normal und Torsionsspannungen in eine Vergleichsspannung um?" Zunächst einmal erzeugen die Querkräfte in diesem Beispiel keine Torsion sondern Schub. Wenn Du es ganz genau machen willst, so fasse Schub- und Normalspannungen zu einem Spannungstensor zusammen, deren Hauptachsrichtungen zu ermitteln sind. In diesen Richtungen wird dann geprüft, ob die ermittelten Spannungen die zulässigen Werte für das gewählte Material nicht überschreiten. Wie das genau geht, müsste ich selbst erst mal nachlesen (zu lange her!). Aber in Euren Skripten und im I-Net sollte doch zu den Themen Vergleichsspannung und Spannungstensor genug beschrieben sein. Das ist Maschinenbau-Standard.

Bei der Art Konstruktion, wie oben beschreiben, halte ich das aber für übertrieben. In der Ausbildung ist das natürlich immer okay.

Knicklasten wären evt. noch ein Thema - bei der Verwendung von dünnwandigen Hohlprofilen oder wenn die tragenden Teile als Fachwerk mit dünnen Stäben ausgelegt werden. Das geht aber in Richtung Leichtbau und ist was für höhere Semester.

ja - und ruhig nachfragen, falls noch was ansteht.

Gruß Werner

---

Hallo Werner,

Die roten Kräfte wo du in der Antwort eingezeichnet hast, sind die Kräfte, die die Rollen auf ihre Lager ausüben hast du geschrieben.

Diese Kräfte sind dann auch die Kräfte wo auf das Gestell wirken. Wie überträgt das Lager dann die Kraft auf das Gestell? Also wie wird die Kraft letztlich übertragen?

Und wie kommt man auf die Richtung dieser Kräfte? Bei A2 zeigt ja die horizontale Kraft bei dir nach links und die vertikale nach unten. Könnte ich es auch anders herum antragen oder geht das nicht? Wenn ich es anders herum antragen würde käme ich am Ende ja z. B. auf andere Schnittreaktion Wie gesagt wie du bei den roten Kräften auf die Richtung kommst ist mir noch nicht ganz klar.

Wäre super wenn du das noch kurz erklären könntest.

Danke schon mal!

---

Hallo Simon,

Du schriebst: "Wie überträgt das Lager dann die Kraft auf das Gestell?"

Schwer für mich heraus zu bekommen, wo genau Du ein Verständnisproblem hast. Das Lager (der Rolle) ist doch mit dem Gestell fest verbunden (davon gehe ich jedenfalls aus!) Also die Antwort könnte sein: "unmittelbar".

Du fragtest: "Und wie kommt man auf die Richtung dieser Kräfte?" Kräfte, die bekannt sind, werden in ihrer wirkenden Richtung eingetragen. Z.B. die Last am Seil mit der Richtung nach unten. Alle unbekannten Kräfte kannst Du frei wählen. Es bietet sich an, aus Gründen der Anschauung, die Kräfte gleich in der Richtung anzunehmen, wie sie voraussichtlich wirken werden. Es hat keinen  Sinn in einem Seil eine Druckkraft anzunehmen und später dann mit einer negativen Druckkraft herum zu rechnen. Ansonsten nimmt man die Komponenten der Kräfte in Richtung eines gewählten Koordinatensystems an. Im Allgemeinen werden - wie auch hier - rechteckige Strukturen vorliegen. Dann legt man sein Koordinatensystem eben parallel zu diesen Richtungen.

Wohlgemerkt bist Du da in  der Wahl frei. Du könntest auch in einem um 30Grad gedrehten Koordinatensystem herum rechnen. Die Achsen des Koordinatensystems müssen noch nicht einmal senkrecht aufeinander stehen. Am Ergebnis sollte dies nichts ändern. Nur ist es eben aufwendiger. Es versteht sich von selbst, dass man eine einmal gewählte Richtung immer beibehalten muss.

Gruß Werner

---

Hallo Werner,

man soll die Lager der Rollen durch eine Bolzenverbindung mit dem Gestell zu verbinden. Also gelangt die Lagerkraft dann über den Bolzen auf das Gestell oder?

Und nach deiner Skizze wirken dann also keine Normalkräfte im Träger oben wirken, da (nach horizontalem Kräftegleichgewicht die Summe der Lagerkräfte zu 0 wird) und als Querkraft dann bei beiden Lagern jeweils S, also eben das Gewicht was am Haken hängt.

Ist das so korrekt?

Wenn du noch kurz was dazu sagen könntest, beenden wir das hier. Hast uns ja schon sehr geholfen! :)

---

Hallo Werner,

ich glaube meine Fragen vom letzten Kommentar ´konnte ich selber beantworten, aber ich bin gerade auf ein neues Problem gest0ßen.

Jetzt mal völlig unabhängig von unserem Kran oben. Angenommen ich habe  ein Stahlprofil, das auf Biegung und auf Zug beansprucht wird. Zunächst möchte ich die Maße des Profils über das Widerstandsmoment ermitteln, indem ich gegen Biegung dimensioniere.

Da gibt es ja die Formel für das erforderliche Widerstandsmoment

W= Maximales Moment / zulässige Spannung.

Sowohl das Moment als auch die zulässige Spannung sind bekannt, also könnte ich mir mein Profil durch die Kenntnis des Widerstandsmoments ausrechnen.

Allerdings würde ich ja mit dieser Formel für W nur die Biegespannungen berücksichtigen und nicht die zusätzlich im Stab noch vorhandene Zugkraft.

ich weiß natürlich, dass man die vorhandene Zugkraft mit der Biegespannung verrechnen könnte, weil Biegung auch nur Zug und Druck erzeugt.  Allerdings würde ja dann die Formel für das Widerstandsmoment W= maximales Moment/ zulässige Spannung nicht mehr funktionieren, da ich ja hier nur das Moment berücksichtigen darf und keine resultierenden Normalspannungen.

Weist du vielleicht wie ich die Zugkraft noch in der Formel berücksichtigen kann?

---

Hallo Simon,

bei Fragen dieser Art muss ich schmunzeln ;-)

Du kennst die Formeln, kennst aber ihre Bedeutung nicht. Das Widerstandsmoment \(W\) gibt Dir ein Maß dafür, wie groß die Spannung \(\sigma_{\max}\) an der kritischen Stelle bei einem gegebenen Moment \(M\) ist - bzw.:

$$\sigma_{\max} = \frac{M}{W} = \frac{M \cdot a_{\max}}{I}$$

\(I\) ist das Flächenträgheitsmoment des Querschnitts und \(a_{\max}\) ist die maximale Entfernung eine Punktes im Querschnitts von der neutralen Faser. Dieses Modell beruht auf der Annahme, dass sich die Spannung bzw. die Dehnung des Materials bei Biegung linear nach 'außen' ausbreitet.

obige Skizze soll ein Balken zeigen, der mit einem Moment belastet ist. Das grüne Feld zeigt den Spannungsverlauf an. Die größte Spannung befindet sich an der Ober- und Unterseite des Balkens.

Kommt nun eine reine Zugspannung hinzu, so wirkt diese gleichmäßig über den gesamten Querschnitt. (zweite grüne Spannungsfeld)

  und die resultierende Spannung (blau) ergibt sich dann aus der Summe der beiden Spannungsverläufe. Das neue \(\sigma_{max}\) ist dann die Summe aus dem \(\sigma_{\max}\) der Biegung plus der Zugspannung - zumindest bei einem symmetrischen Profil (Achtung!).

In der Praxis wählt man ein konkretes Profil und weist anschließend nach, dass die Spannungen den zulässigen Wert nicht überschreiten. Umgekehrt kann man bei der Konstruktion einen Profiltyp wählen (z.B. Rechteckbalken mit festem Verhältnis Höhe zu Breite) und dann die minimale Balkengröße aus der maximal zulässigen Spannung berechnen.

Gruß Werner

---

Hallo Werner,

Danke mal wieder :)

Problem ist nur, dass ich beim Berechnen der resultierenden Spannung (Kraft/Fläche) ja schon den Querschnitt kennen muss, den ich aber erst durch die Formel mit dem Widerstandsmoment berechnen kann.

Heißt ich musste bei der Formel für sigma max sigma zulässig verwenden um auf das Widerstandsmomemt zu kommen.

Ich hab mir dadurch zuerst das Widerstandsmomemt berechnet. Danach dann geprüft ob mein sigma max kleiner als sigma zulässig ist (hier hab ich aber wirklich nur die Spannung durch die biegung berücksichtigt). Abschließend hab ich dann nochmal einen Nachweis für die resultierende Zugspannung gegen Fliesen gemacht (hier hab ich dann die Biegrspannung und die vorhandene Zugspannung addiert) und geprüft ob ich auch hier kleiner sigma zulässig bin.

Kann man das so machen?

---

Jetzt wirklich die letzte Frage Werner ;)

Wenn ich für meine Rollen oben die Wälzlager auswählen möchte muss ich drauf achten das die statische tragzahl des Lagers größer ist als die resultierende kraft wo du in deiner Antwort eingezeichnet hast ist, oder?

---

Du fragtest: ".... kann man das so machen"

Ja - das kann man nicht nur so machen, sondern das sollte man auch so machen. Es wird Dir in der Praxis gar nichts anderes übrig bleiben. Der generelle Weg wird sein, zunächst eine Konstruktion zu schätzen. Dazu berücksichtigt man aus der Erfahrung heraus die kritischen Stellen - in Deinem Fall oben den Punkt X auf Biegung auslegen - plus einer gewissen Sicherheit. Und wenn die gesamte Konstruktion fertig ist, erbringt man noch einmal den Nachweis, dass nirgendwo kritische Spannungen überschritten werden. Und in Deinem Fall ist es völlig richtig die Spannungen aus Zug und Biegung zu addieren und zu sehen dass die Summe kleiner ist als die maximal zulässige Spannung.

Als junger Student hatte ich auch den Anspruch, die Konstruktion 'auszurechnen'. D.h. aus den Lasten und den max. Spannungen die Abmessungen direkt abzuleiten. Und das auch noch auf 4 Stellen hinter dem Komma. Das ist naiv und fern jeder Praxis. Wenn Du damit in die Fertigung gehst und forderst z.B. eine Balkenhöhe von 22,3451mm dann wirst Du nur Gelächter ernten (Wieder so'n Greenhorn von der Uni!). In der Praxis wirst Du einen Katalog von Normprofilen haben aus zwei bis drei unterschiedlichen Materialien und Deine Aufgabe wird es sein, daraus das passende Profil auszuwählen. Dafür gilt es dann den Festigkeitsnachweis zu erbringen.

Und vergiss nicht, dass außer der Festigkeit Dein Kran noch andere Anforderungen erfüllen muss. Um eine Last aufzunehmen muss zwischen den Rollen ausreichend Platz sein. Dann sollte er auch leicht zu manövrieren sein - eventuell an zwei Griffe, die möglichst weit auseinander liegen. Und wenn dort 1500kg dran hängen und hin und her schaukeln ... vielleicht kann man sich was überlegen, um die Last während des Transports zu fixieren. Die vordere Rolle sollte gegen herausspringen des Seils gesichert sein, eventuell schwingend und mit einem Dämpfer versehen aufgehängt werden. usw. es gibt sicher noch mehr zu berücksichtigen.

Zu deiner wirklich letzten Frage*): Ja - und die dynamische auch, falls so was angegeben ist. Auf Grund der Bewegung des Krans über den Boden kann es ja zu Stößen kommen; so etwas gilt es zu berücksichtigen. Gilt natürlich für die gesamte Konstruktion.

Gruß Werner

PS.: *) frag' ruhig weiter; im schlimmsten Fall musst Du zwei bis drei Tage auf die Antwort warten ;-)

---

Ist ja unsere erste Konstruktionsübung. Da ist man schon noch übermotiviert, aber Ich denke unser Grundgestell hält jetzt :)

Wegen der Lagerung. Braucht man da ein Radiallager oder ein Axiallager? Die zwei Möglichkeiten haben wir. Ich habe ja sowohl eine vertikale als auch eine horizontale Lagerkraft (siehe deine Antwort). Radial eigentlich keine Kraft oder?

Wie würdest du die Seilrolle lagern?

---

ganz klar - Radiallager. Du musst natürlich darauf achten, dass diese auch in geringem Maße axiale Kräfte aufnehmen können. Dies ist bei herkömmlichen Rillenkugellagern der Fall. Vielleicht machst Du eine Abschätzung, wie groß diese axiale Kräfte sein können (falls die Last nicht senkrecht aufgenommen wird) und vergleichst sie mit den Angabe in Deinem Lagerkatalog. Kegelwälzlager könnten auch eine Option sein; obwohl die kleiner sind, bei gleicher Tragzahl - das könnte auch ein Kriterium sein. Ich weiß, dass man bei kleineren Rollen Nadellager einbaut. Die nehmen aber keine axialen Kräfte auf und Du wirst mit mindestens. 22kN Last rechnen müssen und das ist nicht von Pappe! Falls das ganze mit dem Rillenkugellager zu groß wird, wäre auch eine asymmetrische Lagerung mit einem Nadel- und einem Rillenkugellager denkbar.

Wichtig: Du brauchst zwei Lager pro Rolle, um eventuelle Kipplasten aufzunehmen oder eben einen Lagertyp, der von Haus aus Kippmomente aufnehmen kann (z.B. zweireihiges Rillenkugellager). Bei Wellen würde man eines der Lager fest und das zweite lose lagern. Da der Lagerabstand aber gering ist und ein seitliches Spiel wahrscheinlich kein Problem ist, kann man sie auch schwimmend lagern. Kann sein, dass dann die Rolle einfacher zu fertigen ist. Noch ein Hinweis: wenn zwei Lager eingebaut werden wird eine axiale Kraft nur von einem der beiden Lager aufgenommen; eine radiale i.A. von beiden,

Und die Schmierung nicht vergessen - hier würde ich sagen: geschlossenes Lager (mit Dichtscheibe), selbstschmierend und wartungsfrei.

Oder eben eine Rolle samt Lager aus einem Katalog aussuchen - ich kenne Eure Vorgaben nicht.

In den üblichen Lagerkatalogen steht i.A. drin, wie man die Lagerauswahl vornimmt. Falls Du selber keinen hast - das I-Net bietet ja genug - hier ist mein erster Treffer und hier der von SKF.

BTW.: darf es auch ein Flaschenzug sein?

Gruß Werner

---

Hallo Werner,

Danke für die Infos! Da muss ich mich auch nochmal genauer informieren wie da die Anforderungen sind. Wir haben ja das ganze Semester für diese Übung Zeit. Zunächst müssen wir eh nur Entwürfe/Zeichnungen/CAD-Modelle etc.  Ich denke das mit der Lagerauswahl krieg ich hin.

Wir müssen ja beim Motor auch für unsere Trommelwelle unsere Lager auswählen. Hier sollen wir eine Fest-Los-Lagerung nehmen. Diese Trommelwelle hat die Aufgabe das Drehmoment von unserem Motor auf unsere Seiltrommel zu übertragen. Demzufolge sollte die Welle eigentlich nur mit einem Torsionsmoment belastet sein oder?

Wie wählt man jetzt hier die Lager aus? Axialkräfte dürfen wir wieder vernachlässigen. Aber hat man hier Radialkräfte? Ich mein Radialkräfte sind ja Kräfte, die senkrecht auf meine Welle wirken. Solche gibt's ja bei unserer Ausführung nicht. Unter was für einen Typ von Beanspruchung fällt also das Dreh bzw. Torsionsmoment vom Motor. Was ich meine ist: Für Axialkräfte brauch ich ein Axiallager, für Radialkräfte ein Radiallager, für Torsion´/Drehmomente brauch ich ein.....? Das ..... ist mir noch nicht ganz klar, also ob ich jetzt ein Radiallager oder Axiallager brauche und warum.

Und in den Lagerkatalogen sind ja immer die Tragzahlen in Newton angegeben. Angaben über zulässige Drehmomente findet man ja meist nicht. Gibt es da eine Vorschrift wie man zum Beispiel das Drehmoment in eine äquivalente Tragzahl umwandeln kann? Wie geht man also hier bei der Lagerauswahl vor, wenn man ein Drehmoment übertragen möchte?

Danke vorab mal wieder! :)

---

Drehlager haben einen Freiheitsgrad um die Drehachse (das macht ein Drehlager aus!) ;-) - also können sie dort auch keine Momente aufnehmen.

Und natürlich wirkt auf die Trommelwelle eine Querkraft und je nach Bauart auch ein Moment senkrecht zur Drehachse; und zwar durch den Seilzug! Und diese Querkraft schlägt voll auf die Lager durch, diese müssen dagegen halten. Du hast also mindestens eine Radialkraft von 7,5kN auf jedem Lager berücksichtigen. Das Drehmoment auf der Welle spielt für die Lagerauswahl keine Rolle. Mit einer großen Trommel hast Du ein großes Moment und mit einer kleinen ein kleines Moment - die Querkraft, die als Radialkraft auf die Lager der Trommelwelle wirkt, ist immer identisch der Querkraft an der Trommel - also hier der Seilkraft.

Wie die Seilkraft (rot) sich auf die beiden Radialkräfte der Lager (blau) verteilt hängt vom Einlaufpunkt des Seils auf der Trommel ab. Dort müssen beide Extremstellungen (links und rechts) berücksichtigt werden.

Gruß Werner

---

.. bevor ich es vergesse: auf beiden Lagern lastet zusätzlich die Querkraft, die aus der Bauart des Motors bzw. Getriebes resultiert. Und die ist nochmal von gleicher Größenordnung.

---

Die Eigengewichte von Motor etc. dürfen wir vernachlässigen. Wie gesagt bei dieser KÜ geht es in erster Hinsicht darum uns mit der Bauteilauslegung vertraut zu machen.

Also hier würdest du dann auch wieder ein Radialkugellager nehmen oder?

Die beiden Extremstellungen wo du angesprochen hast. Ich schau mal ob ich das richtig verstanden hab.

Einmal soll ich so tun wie wenn der Einlaufpunkt des Seils links auf der Trommel ist und für diesen Fall dort die Seilkraft einzeichnen. Dann ein Momentengleichgewicht um diesen Punkt und anschließend die vertikale GG-Bedingung. Dann hab ich ja beide Lagerkräfte. Und das selbe für den Fall dass die erste Seilwindung rechts auf der Seiltrommel gewickelt wird.

Hast du das so gemeint?

---

und durch die Seilkraft wird die Welle ja auch auf Biegung beansprucht oder, was bei deren Dimensionierung wiederum von großer Bedeutung ist oder?

---

Hallo Werner,

Tut mir leid wenn ich schon wieder eine Frage stelle bevor du überhaupt meine letzten Kommentare beantwortet hast ;)

Wir sollen ja die Trommelwelle dimensionieren. Allerdings sehe ich gerade dass wir bereits den Wellendurchnesser und die Größe und Länge der Passfeder vorgegeben haben. Also quasi den Durchmesser von dem Absatz wo in den Motor gesteckt wird mit entsprechenden Passfedermaßen.

Verstehst du was wir hier an der welle noch dimensionieren müssen?

---

Hallo Simon,

Ja - auf jeden Fall Radiallager für die Trommel  - und zwar kräftige, das geht gar nicht anders! Das mit den Extrempositionen habe ich genau so gemeint. Du machst zwei Berechnung. Einmal steht das Seil ganz links und einmal ganz rechts auf der Trommel. Von beiden Ergebnissen nimmst Du jeweils den größeren Wert pro Lager.

Das Gewicht des Motors spielt voraussichtlich keine Rolle. Den wirst Du ja irgendwo festschrauben ;-). Die Frage ist aber: wie leitest Du das Motormoment in die Welle ein? Läuft das über ein Zahnrad oder ein Schneckengetriebe, dann wirken zusätzliche radiale Kräfte in der Größenordnung der Seilkraft. Und die kannst Du unmöglich vernachlässigen. Eine Alternative wäre eine querkraftfreie Kupplung - etwa ein doppeltes Kardangelenk oder eine Schmidt-Kupplung. Das wäre aber ein zusätzlicher Aufwand! Eine Kupplung mit Passfeder und großzügiger Toleranz der Welle kannst Du auch als querkraftfrei annehmen (sehe ich gerade unten).

Die Biegung der Welle, sowohl durch die Seilkraft als auch durch die evt. Radialkraft auf der Motorseite (bei der Kupplung mit Passfeder nicht, da statisch überbestimmt), musst Du natürlich berücksichtigen. Ich erwarte aber nicht, dass das die dominierende Größe ist, da die Lager wahrscheinlich relativ dicht beieinander liegen.

Wenn die Welle mit Durchmesser und Passfeder bereits vorgegeben ist, kannst Du noch was am Material machen und an den Lagerabständen. Einen (Dauer-)Festigkeitsnachweis solltest Du in jedem Fall erbringen.

Noch eine Bemerkung: bei den Verhältnissen würde man wohl eher einen  Flaschenzug installieren. Eine Seilkraft von 15kN auf die Trommel zu bringen, bedeutet nur Aufwand; z.B. beim Getriebe des Motors.

Gruß Werner

---

Hallo Werner,

das Drehmoment wird über eine Passfederverbindung auf die Welle übertragen. Aber das mit der Welle krieg ich schon hin, Danke!

Ich habe nochmal eine Frage zur Bolzenverbindung bei den oberen Umlenkrollen. Es gibt ja diese klassischen 3 Einbaufälle. Ich werde voraussichtlich Einbaufall 1 mit Spielpassung wählen. Aber bei jedem dieser 3 Fälle zeigt ja die Kraft F vertikal nach unten. In deiner Antwort hast du ja schon die Kräfte eingezeichnet, die die Rollen auf ihre Lager ausüben. Die Lager geben ja die Kräfte dann über den Bolzen an das Gestell weiter. Heißt ich habe im Bolzen (wenn ich in der Schnittansicht der 3 Fälle unten im Bild bin) auch eine Kraft S vertikal nach unten und eine Kraft, die aus dem Bildschirm rauszeigt. Das ist ja die horizontale Kraft S aus deiner Antwort.

Kann ich bei der Berechnung der Bolzenverbindung nun trotzdem die Resultierende berechnen (von vertikaler und horizontaler Kraft) und dann gemäß der Fälle im Bild unten annehmen, dass diese Resultierende vertikal nach unten zeigt, um die Formeln der jeweiligen Fälle zu benutzen?

Oder ist es bei den Fällen wirklich wichtig, dass die Resultierende vertikal nach unten zeigt? 

---

Hallo Simon,

entschuldige die späte Antwort - Deine Frage ist inzwischen ein wenig aus meinem Fokus gerückt.

Für die Berechnung an Welle und Bolzen ist es egal, in welche Richtung die Radialkraft zeigt (ein Kreis ist in jeder Ecke gleich rund). Und natürlich musst Du die Resultierende als Kraft annehmen (also wahrscheinlich \(\approx S \sqrt{2}\)).

Bei der Befestigung der Gabel (oder was auch immer) am Rahmen muss dann natürlich die Richtung der Kraft wieder berücksichtigt werden. Wählst Du dort eine Schraubverbindung mit vertikaler Lage der Schrauben, so wird dort eine Kombination aus Zug- und Scherkraft zu berücksichtigen sein.

Gruß Werner

---

Hallo Werner,

Ich hoffe, ich stelle keine zu dummen Fragen für dich, aber wir müssen diese KÜ ohne Kenntnisse aus dem Bereich Maschinenelemente machen. ME hören wir parallel zu unserer KÜ, aber vieles müssen wir schon vor den Vorlesungen in ME anwenden können. :)

Deswegen habe ich nochmal eine Frage zur Befestigung der Trommelwelle mit unserem Gestell. Wir wollen da ein Halteblech auf einen Wellenabsatz schieben, axial natürlich sichern, und dann mit dem Gestell verschrauben. Würden dann in dieser Schraubenverbindung überhaupt Kräfte auf das Gestell übertragen werden? Denn die Welle ist ja bereits mit einer Fest-Los Lagerung ausgestattet (da hast du ja auch schon eine Skizze gezeichnet :)) Heißt diese Lager nehmen ja die Seilkraft schon auf. Die Welle ist ja mit den Lagern dann im Gleichgewicht, weshalb das Blech meiner Meinung nach keine Kraft aufnehmen und übertragen muss. Wie siehst du das?

Was ich mich auch noch Frage. Wenn die Lager die Seilkraft aufnehmen, was passiert dann mit den Kräften in den Lagern? Die Lager sind ja nicht mit dem Gestell verbunden (das wollen wir ja mit einem Halteblech machen). Können die Radiallager die Kräfte, die sie aufnehmen müssen, aufnehmen ohne sie ans Gestell zu übertragen? Sprich kann es einen Kraftfluss innerhalb des Lagers geben, ohne Kraftübertragung ans Gestell?

Vielen Dank im Voraus mal wieder :)

---

Ist Blödsinn was ich geschrieben habe.

Das Halteblech ist natürlich mit der Lagerung verbunden. Damit ist natürlich klar wie die Kräfte ans Gestell übertragen werden.

Angenommen man hat ein Halteblech wo oben und unten jeweils eine Schraube vorgesehen ist. Also das die Schrauben dann quasi parallel zur Wellenachse liegen. Würden die Schrauben dann nur auf Scherung belastet werden? Weil die Lager eben nur Radialkräfte übertragen?

---

Hallo Simon,

Wenn Du die Schrauben nicht fest anziehst, dann ja. Bei 'größeren' Kräften versucht man dies aber zu vermeiden. Dafür gibt es zwei Möglichkeiten: entweder werden zusätzlich Passstifte bzw. Bolzen gesetzt, die die Querkräfte definiert aufnehmen oder es werden Dehnschrauben verwendet, die dann so fest angezogen werden müssen, dass die Querkraft vollständig über die Reibung der Haltebleche auf dem Gestell aufgenommen wird.

Wenn Du Schrauben in dieser Größenordung mit einer Querkraft beaufschlägst, kommt es nach dem Festziehen in der Schraube zu einer Kombination von Zug- und Querkräften, die schwierig zu beherrschen sind. Darüber hinaus hat eine Schraube eine relativ große radiale Toleranz. D.h. die Lage der Einheit Motor, Getriebe und Seiltrommel ist ggf. nicht ausreichend definiert.

---

Hallo Werner,

Danke für die Antwort! Ich denke dass wir mit deinen ganzen Tipps nun zurecht kommen werden.

Eine wirklich letzte Frage hab ich noch. Wenn ich den Ausleger mit dem Galgen (h_max im Bild meiner Frage) mit einer Querstrebe versteifen möchte, wie würden hier die Schnittreaktionen aussehen? Also die Schnittreaktionen in der Querstrebe bzw. welche Kräfte wirken in der Strebe?

Das man so eine Strebe braucht ist mir natürlich klar, nur weiß ich nicht wie das rechnerisch zum Ausdruck kommt.

Vielleicht kannst du das nochmal kurz aufzeigen :)

---

Hallo Simon,

setze die Strebe wie in einem Fachwerk ein. Die Druckkräfte dürften die Momente deutlich übersteigen.

Betrachte \(A\) als Los- und \(B\) als Festlager. Die Querstrebe kann nur Kräfte in Richtung der Strebe aufnehmen. Ab dem Lager \(A\) nach links wird der Querbalken dann wieder wie ein Balken gerechnet - d.h. er muss das Moment aus der Seilkraft aufnehmen.

Vielleicht machst Du für weitere Frage einen neuen Thread auf. Ich habe manchmal Schwierigkeiten diesen hier wieder zu finden.

Gruß Werner

---

Hallo Werner,

Ich hab nur noch eine Frage zu der Strebe. Dann machen wir hier wirklich Schluss :)

Warum nimmt man A als Loslager an und nicht B? Und schneidet man die Querstrebe dann per actio=reactio frei? Heißt die Kräfte im Los und Festlager in umgekehrter Richtung wie bei der Berechnung der Lagerkräfte antragen?Kannst du mir dazu noch ein Freikörperbild zeigen wie man  die inneren Kräfte in der Strebe berechnen würde, wenn ich die Kräfte in A und B kenne?

Und jetzt wirklich die allerletzte Frage in diesem Thread. Du hast ja weiter oben beim FKB der Welle die Seilkraft und die Lagerkräfte eingezeichnet. Die Lagerkräfte werden dann ja ins Gestell übertragen, z. B. über Schrauben.  Müsste man das nicht auch im gesamten Freikörperbild des Krans berücksichtigen? Ganz oben bei den Rollen hast du ja bereits zweimal die Seilkraft eingezeichnet (in der Antwort selbst). Würde durch die Übertragung der Lagerkräfte, was in Summe 15000 N sind, beim Galgen in der Mitte nicht auch eine Querkraft wirken, die nach oben zeigt?

Ich hoffe du weißt was ich meine :)